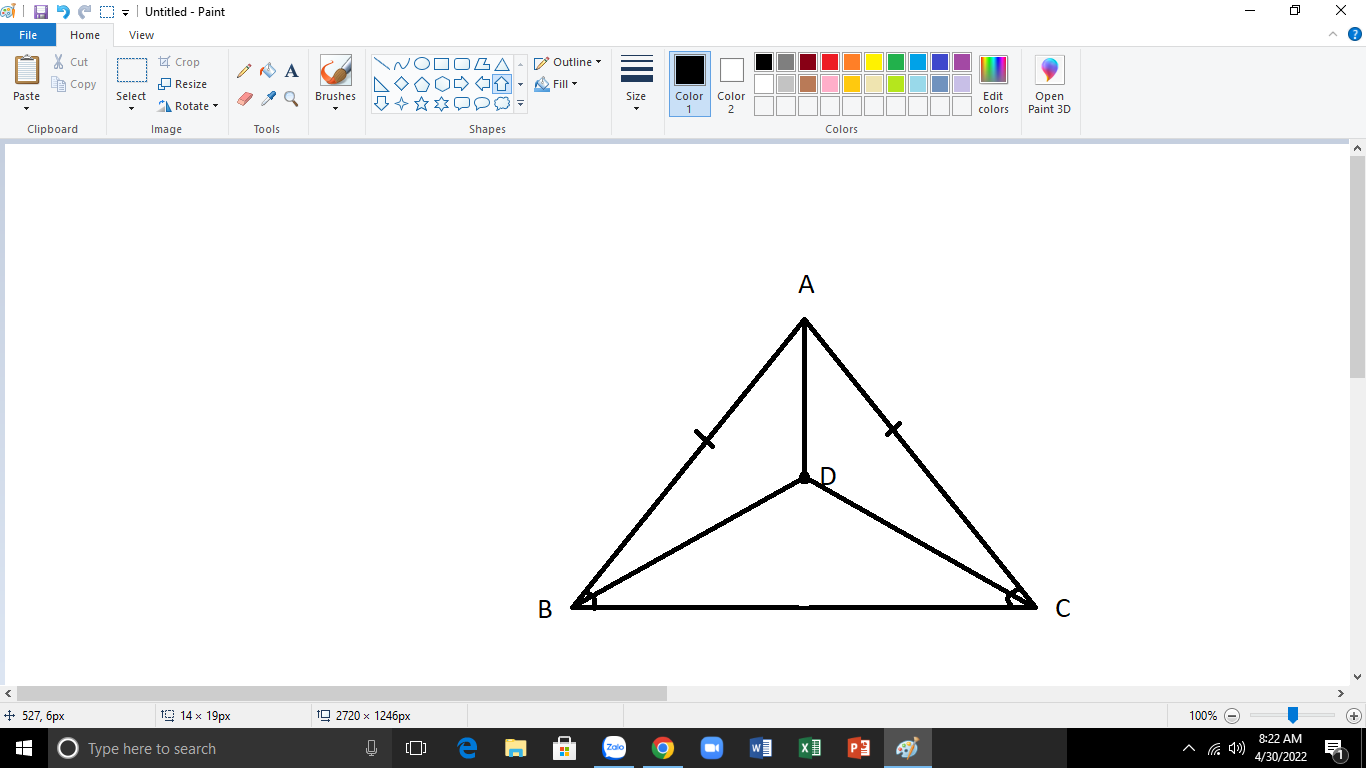
Cho hình 39.
So sánh góc DBC và góc DCB.
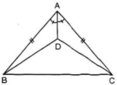
Hình 39
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
4
19 tháng 4 2017
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
19 tháng 4 2017
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210
c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
30 tháng 4 2022
\(\text{a)Xét }\Delta ABD\text{ và }\Delta ACD\text{ có:}\)
\(AB=AC\left(\Delta ABC\text{ cân tại A}\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
\(AD\text{ chung}\)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Ta có:}\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\)
\(\text{Mà }\widehat{ABD}=\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)
H
30 tháng 4 2022
Đây nha:
a. Xét tam giác ABD và tam giác ACD có:
góc BAD = góc BAC (gt)
AD chung
AB = AC (tam giác ABC cân)
=> tam giác ABD = tam giác ACD (cgc)
b. Gọi E là trung điểm của BC
Có: góc BAC = góc BAD + góc CAD mà góc BAD = góc CAD
=> AD là đường phân giác
Lại có: tam giác ABC cân tại A => AD đồng thời là đường trung trực của tam giác ABC
Do đó: DE là đường trung trực cũng là đường phân giác của tam giác BDC.
=> DE vuông với BC tại E; góc BDE = góc CDE
Xét tam giác BDE và tam giác CDE vuông tại E có:
DE chung
góc BDE = góc CDE (cmt)
=> tam giác BDE = tam giác CDE (ch-cgv)
=> góc DBC = góc DCB (2 góc tương ứng)
9 tháng 3 2022
a: Xét ΔBAC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔDBC có BH<CH
mà BH là hình chiếu của DB trên BC
và CH là hình chiếu của DC trên BC
nên DB<DC
=>\(\widehat{DCB}< \widehat{DBC}\)
18 tháng 7 2021
Bài 1:
Vì ∠AOC = ∠BOD (đối đỉnh)
Vì ∠AOC + ∠BOD = 140o (gt)
⇒ ∠AOC = ∠BOD = 140o/2 = 70o
Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)
Thay số: 70o + ∠AOD = 180o
∠AOD = 180o - 70o
∠AOD = 110o
Vì ∠AOD = ∠BOC (đối đỉnh)
⇒ ∠BOC = 110o
Vậy ∠AOC = 70o
∠BOD = 70o
∠AOD = 110o
∠BOC = 110o
L
0
Vì ΔABD = ΔACD (chứng minh câu a)
⇒ BD = CD (hai cạnh tương ứng)
⇒ ΔBCD cân tại D