Tìm cực trị của các hàm số sau: y = x - 6 x 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét trên các miền xác định của các hàm (bạn tự tìm miền xác định)
a.
\(y'=\dfrac{1}{2\sqrt{x-3}}-\dfrac{1}{2\sqrt{6-x}}=\dfrac{\sqrt{6-x}-\sqrt{x-3}}{2\sqrt{\left(x-3\right)\left(6-x\right)}}\)
\(y'=0\Rightarrow6-x=x-3\Rightarrow x=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}\) là điểm cực đại của hàm số
b.
\(y'=1-\dfrac{9}{\left(x-2\right)^2}=0\Rightarrow\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực đại, \(x=5\) là điểm cực tiểu
c.
\(y'=\sqrt{3-x}-\dfrac{x}{2\sqrt{3-x}}=0\Rightarrow2\left(3-x\right)-x=0\)
\(\Rightarrow x=2\)
\(x=2\) là điểm cực đại
d.
\(y'=\dfrac{-x^2+4}{\left(x^2+4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(x=-2\) là điểm cực tiểu, \(x=2\) là điểm cực đại
e.
\(y'=\dfrac{-8\left(x^2-5x+4\right)}{\left(x^2-4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x=1\) là điểm cực tiểu, \(x=4\) là điểm cực đại

Chọn D
![]()
![]()
Hàm số có 2 điểm cực trị x 1 , x 2
![]()
Chia y cho y’ ta được :
![]()
Điểm cực trị tương ứng :
![]()
![]()
Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )
Hai cực trị cùng dấu ⇔ y 1 y 2 > 0
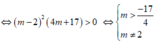
Kết hợp đk : - 17 4 < m < 2

TXĐ: R
y′ = 2(x + 2). x - 3 3 + 3 x + 2 2 . x - 3 2 = 5x(x + 2). x - 3 2
y′= 0 ⇔ 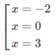
Bảng biến thiên:

Từ đó suy ra y CĐ = y(-2) = 0; y CT = y(0) = -108.
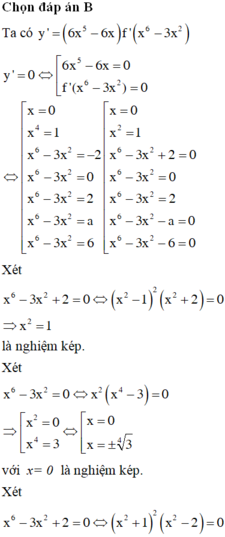
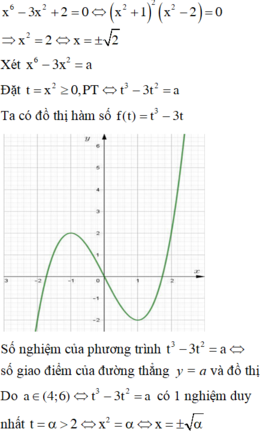

TXĐ: R
y′ = 0 ⇔ x = 64
Bảng biến thiên:
Vậy ta có y CD = y(0) = 0 và y CT = y(64) = -32.