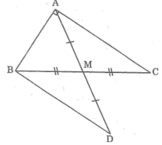
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Tính số đo góc ABD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2019
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
13 tháng 5 2018
a, Xét \(\Delta AMC\) và \(\Delta DMB\) có:
AM = MD ( gt )
\(\widehat{BMD}=\widehat{AMC}\)( hai góc đối đỉnh )
BM = CM ( vì AM là trung tuyến )
\(\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\)
b,\(\Delta AMC=\Delta DMB\left(cmt\right)\Rightarrow\widehat{MBD}=\widehat{C}\)
Xét \(\Delta ABC\) có \(\widehat{A}=90^o\Rightarrow\widehat{ABC}+\widehat{C}=90^o\)(định lý )
mà \(\widehat{MBD}=\widehat{C}\Rightarrow\widehat{ABC}+\widehat{MBD}=90^o\)
hay \(\widehat{ABD}=90^0\)
c,\(\Delta AMC=\Delta DMB\left(cmt\right)\Rightarrow BD=AC\)
Xét \(\Delta ABC\) và \(\Delta BAD\) có:
AB cạnh chung
\(\widehat{ABD}=\widehat{BAC}=90^o\)
BD = AC ( cmt )
\(\Rightarrow\Delta ABC=\Delta BAD\left(c.g.c\right)\)
\(\Rightarrow BC=AD\)
Vì AM = MD => \(AM=\frac{1}{2}AD\)
mà BC = AD ( cmt )
\(\Rightarrow AM=\frac{1}{2}BC\)
TB
2 tháng 8 2015
a) tam giác MAC = tam giác BAD theo trường hợp cạnh góc cạnh
Có: MC = MB (AM trung tuyến)
AMC = DMB (2 góc đối đỉnh)
MA = MD (theo giả thiết)
=> 2 tam giác bằng nhau theo trường hợp cạnh góc cạnh
b)
Tam giác ABC có góc A=90 độ
Suy ra: góc ACB+ góc CBA= 90 độ
Mà : góc ACB (hay góc ACM) = DBM (2 tam giác bằng nhau, chứng minh trên)
Suy ra: góc DBM + CBA = 90 độ
Hay DBA=90 độ
Xét ΔAMC và ΔDMB, ta có:
CM = BM (gt)
∠(AMC) = ∠(BMD) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy ∠(ABD) = 90o.