Một cây cọc dài được cắm thẳng đứng xuống một bể nước chiết suất n = 4 3 . Phần cọc nhô ra ngoài mặt nước là 30 cm, bóng của nó trên mặt nước dài 40 cm và dưới đáy bể nước dài 190 cm. Tính chiều sâu của lớp nước.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
30 tháng 10 2018
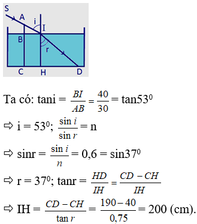
Ta có:
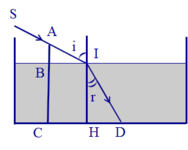
tan i = B I A B = 40 30 = tan 53 ° ; sin i sin r = n ⇒ sin r = sin i n = 0 , 6 = sin 37 ° ⇒ r = 37 ° ; tan r = H D I H = C D - C H I H ⇒ I H = C D - C H tan r = 190 - 40 0 , 75 = 200 ( c m ) .
VT
26 tháng 10 2018
Đáp án C
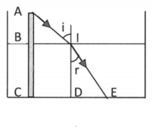
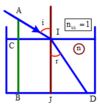
Gọi AB là phần cọc nhô lên mặt nước; BC là phần cọc ngập trong nước; BI là bóng của cọc trên mặt nước; CE là bóng của cọc dưới đáy bể.
- Chiều sâu của bể nước:
VT
22 tháng 3 2019
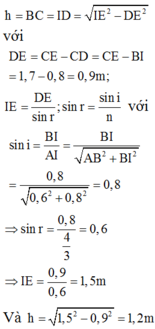
Đáp án C
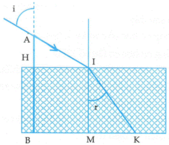
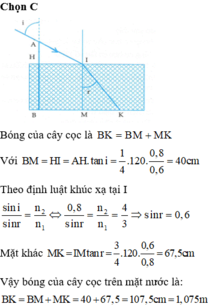
Bóng của cây cọc là B K = B M + M K
Với
Theo định luật khúc xạ tại I
Mặt khác
Vậy bóng của cây cọc trên mặt nước là:
VT
29 tháng 3 2018
Đáp án C
Bóng của cây cọc là B K = B M + M K
Với B M = H I = A H tan i = 1 4 .120. 0 , 8 0 , 6 = 40 c m
Theo định luật khúc xạ tại I
sin i sin r = n 2 n 1 ⇔ 0 , 8 sin r = n 2 n 1 = 4 3 ⇒ sin r = 0 , 6
Mặt khác: M K = I M tan r = 3 4 .120. 0 , 6 0 , 8 = 67 , 5 c m
Vậy bóng của cây cọc trên mặt nước là:
B K = B M + M K = 40 + 67 , 5 = 107 , 5 c m = 1 , 075 m
VT
13 tháng 10 2018
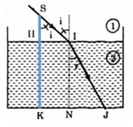
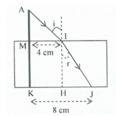
Từ hình vẽ ta có:
HS = 4cm
HI =4 cm
KJ =8 cm
NJ = KJ – KN = KJ – HI = 8 – 4 = 4cm
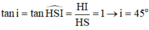
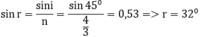
Chiều sâu của lớp nước trong bình:
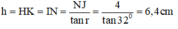
Đáp số: h = 6,4 cm
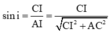
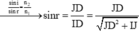
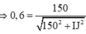
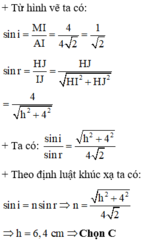
Vậy chiều sâu của lớp nước là 200 cm.