Cho tam giác ABC, các đường phân giác của các góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân đường vuông góc kẻ từ E đến các đường thẳng BC, AB, AC. Chứng minh AE là tia phân giác của góc BAC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 7 2019
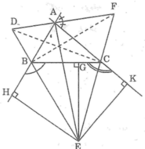
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
CM
17 tháng 5 2019
Ta có: BF là tia phân giác góc trong tại đỉnh B
BE là tia phân giác góc ngoài tại đỉnh B
Suy ra: BF ⊥ BE (tính chất hai góc kề bù)
Vậy BF ⊥ ED.
Lại có: CD là đường phân giác góc ngoài tại C
CE là đường phân giác góc trong tại C
Suy ra: CD ⊥ CE (tính chất hai góc kề bù)
Vậy CD ⊥ EF.
Vậy các đường thẳng EA; FB; DC là các đường cao trong tam giác DEF.
29 tháng 7 2017
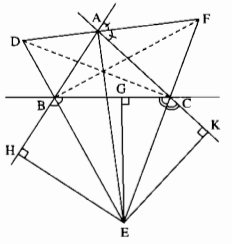
a) E thuộc tia phân giác của CBH^
⇒ EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của BCK^
⇒ EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
⇒ E thuộc tia phân giác của BAC^ mà E # A
Vậy AE là tia phân giác của BAC^
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
⇒ AE⊥AF (tính chất hai góc kề bù)
Hay AE⊥DF
d) Chứng minh tương tự câu a ta có BF là tia phân giác của ABC^
CD là tia phân giác của ACB^
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
⇒BF⊥BE (tính chất hai góc kề bù)
Hay BF⊥ED
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
⇒CD⊥CE (tính chất hai góc kề bù)
Hay
24 tháng 2 2018
a) E thuộc tia phân giác của ˆCBHCBHˆ
⇒⇒ EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ˆBCKBCKˆ
⇒⇒ EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
⇒⇒ E thuộc tia phân giác của ˆBACBACˆ mà E # A
Vậy AE là tia phân giác của ˆBACBACˆ
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
⇒⇒ AE⊥AFAE⊥AF (tính chất hai góc kề bù)
Hay AE⊥DFAE⊥DF
d) Chứng minh tương tự câu a ta có BF là tia phân giác của ˆABCABCˆ
CD là tia phân giác của ˆACBACBˆ
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
⇒BF⊥BE⇒BF⊥BE (tính chất hai góc kề bù)
Hay BF⊥EDBF⊥ED
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
⇒CD⊥CE⇒CD⊥CE (tính chất hai góc kề bù)
Hay CD⊥EF
CM
18 tháng 12 2017
Ta có: E thuộc tia phân giác của ∠(CBH)
Suy ra: EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ∠(BCK)
QUẢNG CÁOSuy ra: EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK.
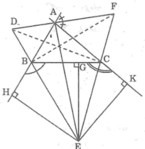
Ta có: EH = EK (chứng minh trên)
Suy ra: E thuộc tia phân giác của ∠(BAC).
Mà E khác A nên AE là tia phân giác của ∠(BAC)