Một ô tô có khối lượng 1 tấn chuyển động trên đường ngang khi qua A có vận tốc 18km/h và đến B cách A một khoảng là 100m với vận tốc 54km/h.
a. Tính công mà lực kéo của động cơ đã thực hiện trên đoạn đường AB.
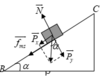
b. Đến B tài xế tắt máy và xe tiếp tục xuống dốc nghiêng BC dài 100m, cao 60m. Tính vận tốc tại C.
c. Đến C xe vẫn không nổ máy, tiếp tục leo lên dốc nghiêng CD hợp với mặt phẳng nằm ngang một góc 30o. Tính độ cao cực đại mà xe đạt được trên mặt phẳng nghiêng này. Cho biết hệ số ma sát không thay đổi trong quá trình chuyển động của xe là µ = 0,1, lấy g = 10ms-2.

a. Ta có
v A = 18 ( k m / h ) = 5 ( m / s ) ; v B = 54 ( k m / h ) = 15 ( m / s )
Áp dụng định lý động năng
A = 1 2 m v B 2 − 1 2 m v A 2 ⇒ A F → + A f → m s = 1 2 m ( v B 2 − v A 2 )
Mà A f m s = − f m s . s = − μ . N . s = − μ . m . g . s = − 0 , 1.1000.10.100 = − 10 5 ( J ) ⇒ A F → = 1 2 .1000 ( 15 2 − 5 2 ) + 10 5 = 2.10 5 ( J )
b. Ta có
sin α = 60 100 = 3 5 ; cos α = 100 2 − 60 2 100 = 4 5
Áp dụng định lý động năng
A = W d C − W d B ⇒ A P → + A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công của trọng lực
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 1000.10. 3 5 .100 = 6.10 5 ( J )
Công của lực ma sát
A f m s = − f m s . B C = − μ N . B C = − μ . m g cos α . B C A f m s = − 0 , 1.1000.10. 4 5 .100 = − 8.10 4 ( J )
⇒ 6.10 5 − 8.10 4 = 1 2 .1000. ( v C 2 − 15 2 ) ⇒ v C = 35 , 57 ( m / s )
c. Gọi E là vị trí mà xe có thể lên được
v E = 0 ( m / s )
Áp dụng định lý động năng
A = W d E − W d C ⇒ A P → + A f → m s = − 1 2 m v C 2
Công trọng lực của vật
A P → = − P x . C E = − m g sin 30 0 . C E ⇒ A P → = − 1000.10. 1 2 . C E = − 5000. C E ( J )
Công của lực ma sát
A f m s = − f m s . C E = − μ N . C E = − μ . m . g cos 30 0 . C E = − 500 3 . C E ( J )
⇒ − 5000. C E − 500 3 . C E = − 1 2 .1000. ( 35 , 57 ) 2 ⇒ C E = 107 , 8435 ( m )