Tìm các tam giác bằng nhau ở hình dưới (không xét tam giác mà các cạnh chưa được kẻ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 6 2017
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
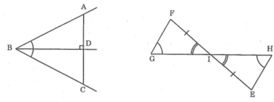
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH
13 tháng 10 2017
Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha
CM
7 tháng 8 2019
Đáp án A
Số tam giác tạo bởi các đỉnh của đa giác là C 7 3 = 35
Số tam giác có 2 cạnh là 2 cạnh của đa giác là 7
Số tam giác có 1 cạnh là cạnh của đa giác là 7.3 = 21
Vậy số tam giác tạo bởi đỉnh của đa giác và không có cạnh trùng với cạnh của đa giác là 35 - (7 + 21) = 7 tam giác.
CM
11 tháng 3 2018
Đáp án A
Số tam giác tạo bởi các đỉnh của đa giác là C 7 3 =35
Số tam giác có 2 cạnh là 2 cạnh của đa giác là 7
Số tam giác có 1 cạnh là cạnh của đa giác là 
Vậy số tam giác tạo bởi đỉnh của đa giác và không có cạnh trùng với cạnh của đa giác là 
tam giác.
10 tháng 10 2023
a) Chỉ có ABC là hình có 3 cạnh bằng nhau.
b) Các góc của tam giác ABC bằng nhau và đều bằng \(60^\circ \) .
CM
19 tháng 1 2019
- Xem hình 63)
Ta có:
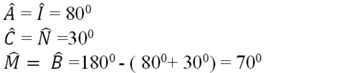
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO- Xem hình 64)
ΔPQR có:
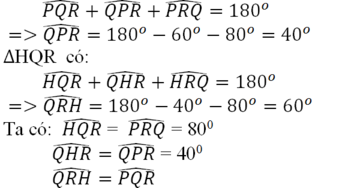
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
+ ΔABD = ΔCBD (g.c.g) vì:
∠ABD = ∠CBD (gt)
BD chung
∠ADB = ∠BDC (= 90o)
+ Ta có: ∠FGI = ∠IHE ( giả thiết). Mà hai góc này ở vị trí so le trong nên: FG // HE
⇒ ∠GFI = ∠IEH ( hai góc so le trong).
*) Khi đó: ΔGIF = ΔHIE (g.c.g) vì:
∠GFI = ∠IEH ( chứng minh trên)
FI = IE ( giả thiết)
∠GIF = ∠EIH (hai góc đối đỉnh)