Cho đoạn thẳng AB dài 4cm Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm, chúng cắt nhau ở C và D, chứng minh rằng AB là tia phân giác của góc CAD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 3 2016
∆BAC và ∆ BAD có: AC=AD(gt)
BC=BD(gt)
AB cạnh chung.
Nên ∆ BAC= ∆ BAD(c.c.c)
Suy ra BAC = BAD (góc tương ứng)
Vậy AB là tia phân giác của góc CAD
CT
15 tháng 11 2018
Noi AC ;BC;AD;BD
Xét tam giác ACB và tam giác ADB , ta co:\
CA=AD ( BK của A )
CB=DB (BK cua B )
Canh AB chung
=>tam giac ACB=tam giac ADB (c.c.c)
=>goc CAB =goc BAD
ma tia AB nam giua 2 tia AC,AD
=>tia AB la phan giac cua goc CAD
18 tháng 10 2017
Xét có :
AB chung
AC = AD (gt)
BC=BD
=> tam giác BAC = BAD ( c.c.c )
=> góc BAC = BAD ( 2 góc tương ứng)
=> AB là tia phân giác của góc CAD
15 tháng 11 2017
Vì C là giao của đường tròn tâm A và tâm B nên AC=2cm,BC=3cm
Vì D là giao của đường tròn tâm A và tâm B nên AD=2cm,BD=3cm
Do đó AC=AD,BC=BD
Xét ΔBAC và ΔBAD có:
+) AC=AD
+) BC=BD
+) AB cạnh chung.
Suy ra ΔBAC=ΔBAD(c.c.c)
Suy ra ˆBAC = ˆBAD (hai góc tương ứng)
Vậy AB là tia phân giác của góc CAD
HH
20 tháng 4 2017
∆BAC và ∆ BAD có: AC=AD(gt)
BC=BD(gt)
AB cạnh chung.
Nên ∆ BAC= ∆ BAD(c.c.c)
Suy ra ˆBACBAC^ = ˆBADBAD^(góc tương ứng)
Vậy AB là tia phân giác của góc CAD
L
5 tháng 11 2019
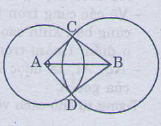
Tự vẽ hình >:
Nối BC, nối BD
Xét ΔACB và ΔADB có:
AC=AD vì C, D thuộc (A; 3cm)
AB: canh chung
BD=BC vì C, D thuộc (B; 4cm)
=>ΔACB=ΔADB(c.c.c)
=>^CAB=^BAD(hai góc tương ứng)
=>AB là pg ^CAD(đpcm)
5 tháng 11 2019
AC=AD vì C, D thuộc (A;3cm) với
BD=BC vì C,D thuộc (B;4cm) là sao z bn
Còn đpcm là gì
5 tháng 11 2017
Bạn tự vẽ hình nhé!
Xét \(\Delta\)CAB và DAB có:
AC=AD(=2cm)
CB=DB(=3cm)
AB là cạnh chung
\(\Rightarrow\)\(\Delta\)CAB=\(\Delta\)DAB (c.c.c)
\(\Rightarrow\)\(\widehat{A_1}\)=\(\widehat{A_2}\)
Vậy AB là tia phân giác của\(\widehat{CAD}\)(đpcm)
Nối BC, BD, AC, AD.
ΔABC và ΔABD có:
AC = AD (=2cm)
BC = BD (=3cm)
AB cạnh chung
Nên ΔABC = ΔABD (c.c.c)
Suy ra góc CAB = góc DAB (góc tương ứng)
⇒ AB là tia phân giác của góc CAD