Cho hai hàm số y = 3 2 x 2 và y = - 3 2 x 2 . Điền vào chỗ trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
| x | -2 | -1 | 0 | 1 | 2 |
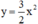 |
| x | -2 | -1 | 0 | 1 | 2 |
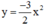 |
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x+3=x+2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{7}{3}\end{matrix}\right.\)

| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 1/2 x2 | 9/2 | 2 | 1/2 | 0 | 1/2 | 2 | 9/2 |
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = (-1)/2 x2 | (-9)/2 | -2 | (-1)/2 | 0 | (-1)/2 | -2 | (-9)/2 |

Lời giải:
a.
Đồ thị xanh lá: $y=2x+1$
Đồ thị xanh dương: $y=x-3$
b.
PT hoành độ giao điểm:
$y=2x+1=x-3$
$\Leftrightarrow x=-4$
$y=x-3=(-4)-3=-7$
Vậy tọa độ điểm $M$ là $(-4;-7)$

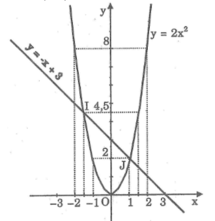
*Vẽ đồ thị hàm số y = 2 x 2
| x | -2 | -1 | 0 | 1 | 2 |
| y = 2 x 2 | 8 | 2 | 0 | 2 | 8 |
*Vẽ đồ thị hàm số y = -x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = 3 ⇒ (3; 0)
+ Điền vào ô trống:
Vậy ta có bảng:
Tương tự như vậy với hàm số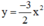 . Ta có bảng:
. Ta có bảng:
+ Vẽ đồ thị hàm số:
Trên mặt phẳng lưới lấy các điểm A(-2; 6);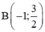 ; O(0; 0);
; O(0; 0); 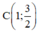 ; D(2; 6).
; D(2; 6).
Nối các điểm trên theo một đường cong ta được parabol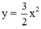
Lấy các điểm A’ (-2; -6);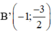 ; O(0; 0);
; O(0; 0); 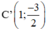 ; D’(2; -6).
; D’(2; -6).
Nối các điểm trên theo một đường cong ta được parabol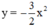
Nhận xét: Đồ thị hàm số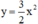 và
và 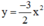 đối xứng nhau qua trục Ox.
đối xứng nhau qua trục Ox.