Cho hai đường tròn (O) và (O’) tiếp xúc với nhau tại A như hình bên. Chứng minh rằng các bán kính OB và O’C song song với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
26 tháng 5 2018
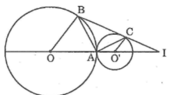
Ta có : OB // O’C (gt)
Suy ra : (hai góc trong cùng phía)
OA = OB (=R)
⇒ Tam giác AOB cân tại O

16 tháng 5 2022
Ta có: ΔO'AC cân tại O'
nên \(\widehat{CO'A}=180^0-2\cdot\widehat{A}\)(1)
Ta có: ΔOBA cân tại O
nên \(\widehat{BOA}=180^0-2\cdot\widehat{A}\)(2)
Từ (1) và (2) suy ra \(\widehat{CO'A}=\widehat{BOA}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên O'C//OB

CM
22 tháng 1 2019
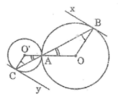
a, Sử dụng AQ//O'P
=> Q A P ^ = O ' A P ^ => Đpcm
b, CP//BR (cùng vuông góc AR)

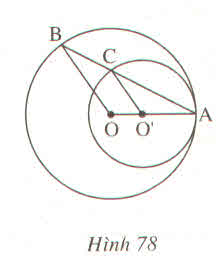
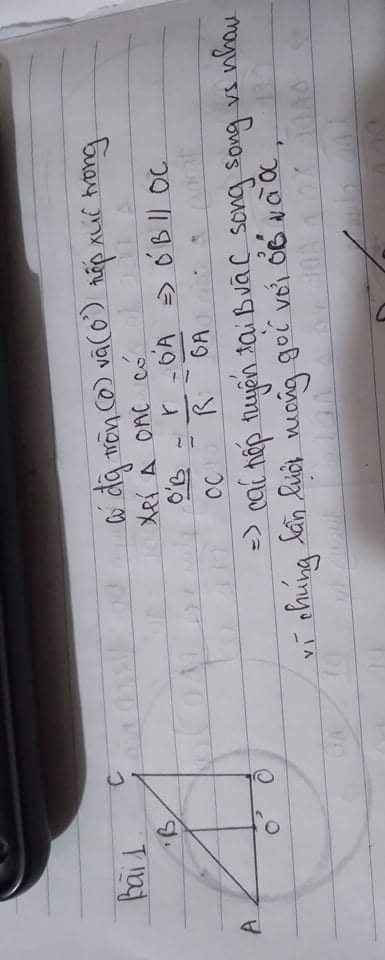
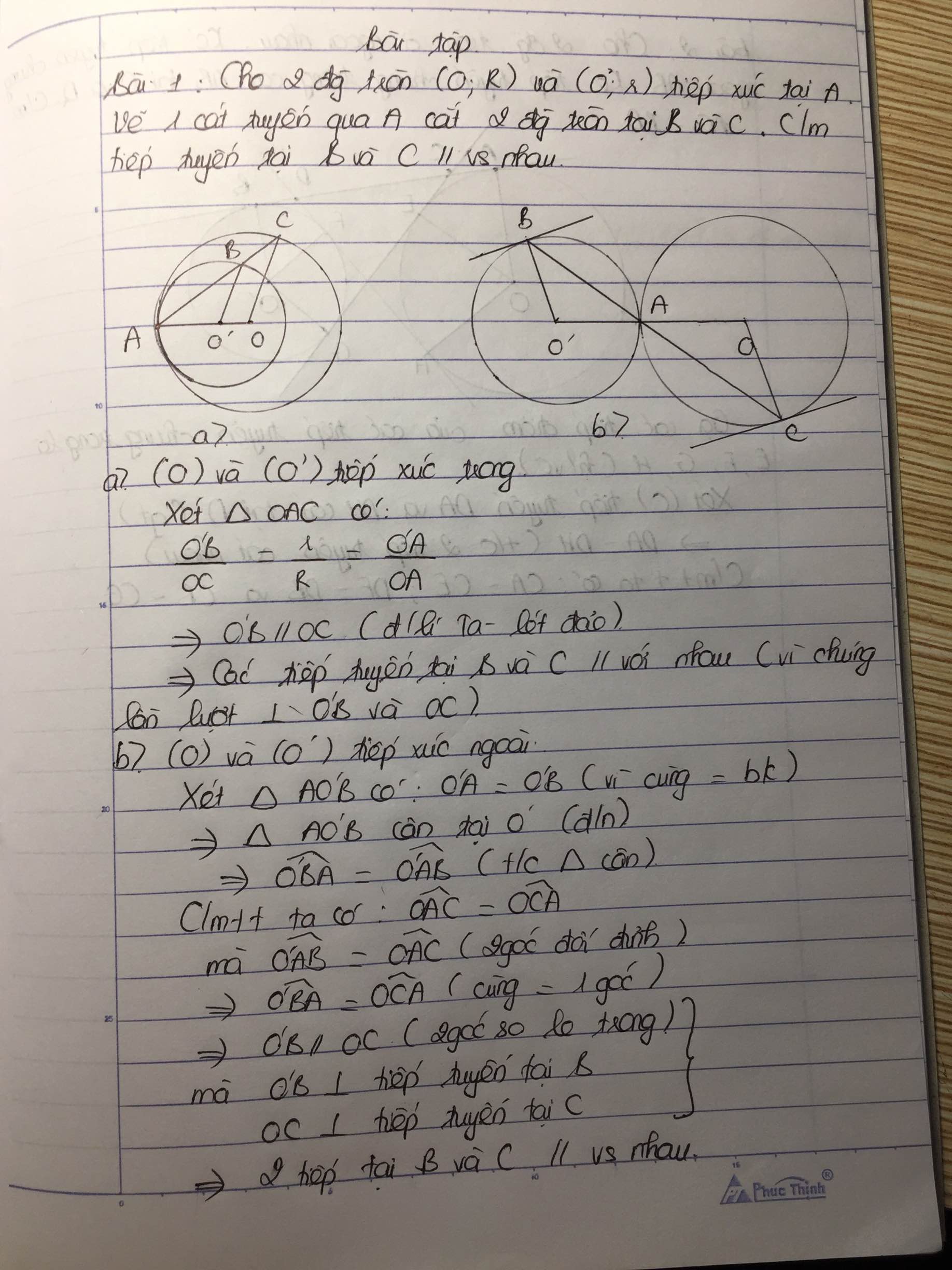
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)