Cho tam giác ABC có cạnh BC cố định và góc A = α không đổi.Tìm quỹ tích giao điểm của ba đường phân giác trong cuả tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án D
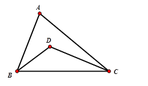
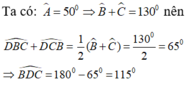
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC

Chọn đáp án D
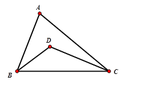
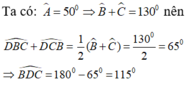
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC

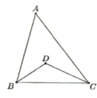
Ta có A ^ = 50 0 ⇒ B ^ + C ^ = 130 0
D B C ^ + D C B ^ = 65 0 ⇒ B D C ^ = 115 0
=> Quỹ tích của điểm D là hai cung chứa góc 115 0 dựng trên đoạn BC

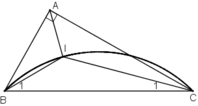
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135 º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135 º dựng trên đoạn BC.
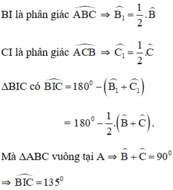
⇒ I thuộc cung chứa góc 135 º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135 º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135 º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của 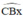
+ Kẻ tia Cy sao cho CI là phân giác của 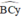
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135 º dựng trên đoạn BC (khác B và C).
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước :
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích : gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm M thỏa mãn 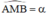 (với A, B cố định, α không đổi) là cung chứa góc α dựng trên đoạn AB. (Cách dựng xem SGK).
(với A, B cố định, α không đổi) là cung chứa góc α dựng trên đoạn AB. (Cách dựng xem SGK).

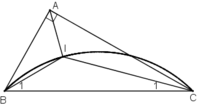
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135º dựng trên đoạn BC.
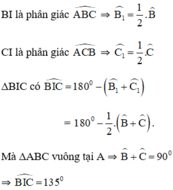
⇒ I thuộc cung chứa góc 135º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của 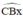
+ Kẻ tia Cy sao cho CI là phân giác của 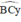
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
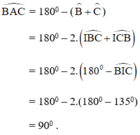
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135º dựng trên đoạn BC (khác B và C).

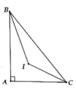
Tương tự câu 1
Tính được B I C ^ = 135 0
=> Quỹ tích của điểm I là hai cung chứa góc 135 0 dựng trên đoạn BC

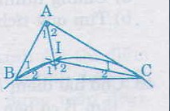
Theo tính chất của góc ngoài tam giác, ta có;
\(\widehat{I_2}=\widehat{A_1}+\widehat{B_1}\) (1)
\(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\) (2)
Cộng vế (1) và (2) vế với vế:
\(\widehat{I_1}+\widehat{I_2}=\widehat{A_1}+\widehat{A_2}+\widehat{B_1}+\widehat{C_1}\)
Hay \(\widehat{I}=90^o+45^o=135^o\)
Điểm I nhìn đoạn thẳng BC cố định dưới góc 135o không đổi, vậy quỹ tích của I là góc cung chứa góc 135o dựng trên đoạn thẳng BC
Một CTV gương mẫu chưa từng thấy! :)
Vậy mà cũng là CTV học tập! :)

*Chứng minh thuận:
Gọi I là giao điểm của ba đường phân giác trong của tam giác ABC