Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
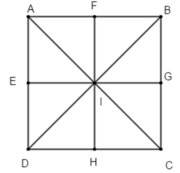
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

V ( C ; 2 ) ( I G H F ) = ( A I F D ) ; Đ I ( A I F D ) = C I E B .
Đáp án C.

Đ E I ( 1 ) = ( 8 ) ; T D I → ( 8 ) = ( 3 ) .
A. Phép đối xứng tâm I và phép đối xứng trục IB thì (1) không biến thành hình nào từ (2) đến (8).
B. Phép đối xứng tâm I và phép quay tâm I góc quay 90 o (1) không biến thành hình nào từ (2) đến (8)
D.phép tịnh tiến theo A I → và phép đối xứng tâm I thì hình (1) thành hình (2)
Đáp án C

Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng

\(Ta\) \(có\) \(S_{ABCD}=6.6=36\left(cm^2\right)\)
\(S_{EFGH}=\dfrac{1}{2}S_{ABCD}=\dfrac{1}{2}.36=18\left(cm^2\right)\)
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H.
Chọn đáp án C