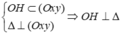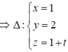Trong mặt phẳng tọa độ Oxy, xét họ đường thẳng (dm) cho bởi phương trình \(\left(m-1\right)x+my=m\)tính khoảng cách từ điểm gốc ) đến đường thẳng (dm)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(d\left(M;\Delta\right)=\dfrac{\left|6-9\right|}{\sqrt{1^2+2^2}}=\dfrac{3\sqrt{5}}{5}\)
b, Đường tròn cần tìm có bán kính \(R=d\left(M;\Delta\right)=\dfrac{3\sqrt{5}}{5}\), tâm \(M=\left(6;0\right)\)
Phương trình đường tròn: \(\left(x-6\right)^2+y^2=\dfrac{9}{5}\)

a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .

Xét m=4 =>(d):y=1 =>Khoảng cách từ gốc tọa độ đến đt (d) khi đó là 1
Xét m=3 =>(d):x=-1=> Khoảng cách từ gốc tọa độ đến đt (d) khi đó là 1
Xét \(m\ne4;m\ne3\)
Gọi \(A=Ox\cap\left(d\right)\) \(\Rightarrow A\left(\dfrac{1}{m-4};0\right)\), \(B=Oy\cap\left(d\right)\Rightarrow B\left(0;\dfrac{1}{m-3}\right)\)
Gọi H là hình chiếu của O lên AB
Có \(OH^2=\dfrac{OA^2.OB^2}{OA^2+OB^2}=\dfrac{\left(\dfrac{1}{m-4}\right)^2.\left(\dfrac{1}{m-3}\right)^2}{\left(\dfrac{1}{m-4}\right)^2+\left(\dfrac{1}{m-3}\right)^2}\)
\(=\dfrac{1}{\left(m-4\right)^2\left(m-3\right)^2\left[\dfrac{1}{\left(m-4\right)^2}+\dfrac{1}{\left(m-3\right)^2}\right]}\)
\(=\dfrac{1}{\left(m-4\right)^2+\left(m-3\right)^2}\)
\(=\dfrac{1}{2m^2-14m+25}=\dfrac{1}{2\left(m-\dfrac{7}{2}\right)^2+\dfrac{1}{2}}\le2\)
=> \(OH\le\sqrt{2}\)
=> Khoảng cách lớn nhất gốc tọa độ đến (d) là \(\sqrt{2}\Leftrightarrow m=\dfrac{7}{2}\) (thỏa)
Xét điểm \(A\left(-1;1\right)\). Dễ thấy A thuộc (d). Gọi H là hình chiếu của O trên (d). Ta có \(OH\le OA=\sqrt{2}\). Dấu "=" xảy ra khi và chỉ khi \(H\equiv A\), tức là \(d\perp OA\).
Ta cần tìm m sao cho \(d\perp OA\). Phương trình đường thẳng đi qua O, A là
y = -x. Xét m = 4 thì đường thẳng (d) trở thành \(y=1\), đường thẳng này song song với trục hoành và không vuông góc với d. Xét m khác 4. Khi đó \(\left(m-4\right)x+\left(m-3\right)y=1\Leftrightarrow y=\dfrac{4-m}{m-3}x+\dfrac{1}{m-3}\). Để \(d\perp OA\) thì \(\dfrac{4-m}{m-3}.\left(-1\right)=-1\Leftrightarrow4-m=m-3\Leftrightarrow m=\dfrac{7}{2}\).
Vậy Max \(OH=\sqrt{2}\Leftrightarrow m=\dfrac{7}{2}\).

b) Xét tam giác OMB vuông tại O có:
BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2
Tương tự tam giác OAB vuông tại O có:
B A 2 = O A 2 + O B 2 = 1 + 1 = 2 ⇒ BA = 2
Xét tam giác MAB có:
B M 2 + B A 2 = 2 + 2 = 4 = A M 2
⇒ ΔMAB vuông tại B
Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = 2