Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh bằng a. Tính diện tích toàn phần và thể tích hình nón đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Độ dài đường sinh là l = a .
Bán kính đáy là: R = a 2 + a 2 2 = a 2 2
Diện tích toàn phần của hình nón là: S = π R 2 + π R l = π a 2 2 2 + π a 2 2 . a = π 1 + 2 a 2 2

Đáp án A
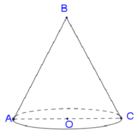
Thiết diện là tam giác vuông cân tại đình B, cạnh huyền AC = 2.

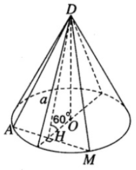
Xét mặt phẳng (DAM) đi qua đỉnh D tạo với mặt phẳng đáy một góc 600, cắt đường tròn đáy tại hai điểm A và M. Từ tâm O của đường tròn đáy ta vẽ OH ⊥ AM, do vậy H là trung điểm của đoạn AM. Ta có AM ⊥ (DOH) vì AM ⊥ OH và AM ⊥ DO.
Vậy
∠
DHO = 60
°
và 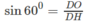
hay 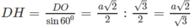
Gọi SΔ DAM là diện tích thiết diện cần tìm, ta có: S △ DAM = AH.DH
Mà ![]()
![]()
Vậy
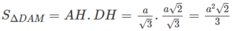

Chọn B.
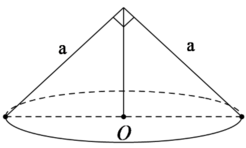
Thiết diện qua trục là một tam giác vuông cạnh a nên đường sinh của hình nón là l = a.
Đường kính của đường tròn đáy là:
![]()
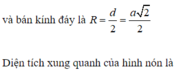
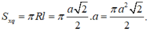



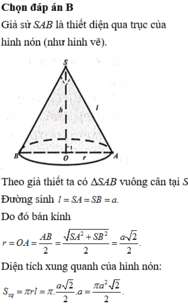
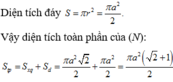
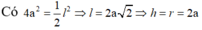
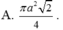
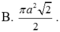
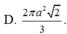
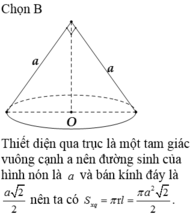
Thiết diện qua trục của hình nón là tam giác vuông cân cạnh a nên hình nón có đường sinh l = a,
có bán kính đáy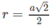
và có chiều cao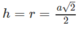
Gọi S xq là diện tích xung quanh của hình nón, ta có:
Gọi S là diện tích đáy của hình nón, ta có
Vậy diện tích toàn phần của hình nón đã cho là:
Hình nón có thể tích là: