Cho hình vuông ABCD. Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng nằm trên một đường tròn
b: Tâm là trung điểm của AC

a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
\(R=\dfrac{AC}{2}\)

a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
b: Tâm là trung điểm của AC
Bán kính là \(\dfrac{a\sqrt{2}}{2}\)

a: Xét tứ giác ABCD có
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC

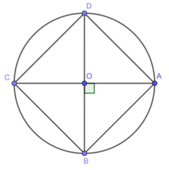
*Cách vẽ:
- Vẽ đường tròn tâm O bán kính 1,5cm
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB, BC , CD, DA lại với nhau ta được hình vuông ABCD nội tiếp trong đường tròn (O; 1,5)
*Chứng minh:
Ta có : OA = OC , OB =OD
Suy ra ABCD là hình bình hành
Mặt khác : AC = BD và AC ⊥ BD
Suy ra ABCD là hình vuông

Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.