Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
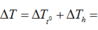
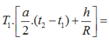
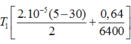
ΔT < 0 đồng hồ chạy nhanh
+ Mỗi chu kỳ đồng hồ chỉ sai thời gian ΔT => Một ngày đêm đồng hồ chạy nhanh:
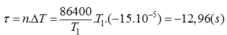
Đáp án A
Con lắc chịu 2 sự biến đổi: Sự nở dài về nhiệt và sự thay đổi độ cao. Ta có:
Theo đề bài, đồg hồ chạy đúng giờ nên T 1 = T 2 và ∆ T = 0
Suy ra
Chọn A
+ Đồng hồ chạy đúng khi tổng các sai lệch về chu kỳ bằng 0:
=>
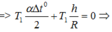
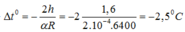
Đáp án D
+ Chu kì dao động riêng của con lắc trong không khí và trong chân không được xác định bởi:
.
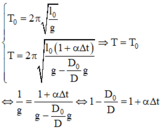
Thay các giá trị vào biểu thức, ta tìm được:
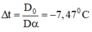
Vậy nhiệt độ của hộp chân không là 17 , 5 ° C .
Đáp án A
Con lắc chịu hai sự biến đổi: sự nở dài về nhiệt và sự thay đổi độ cao.
Ta có:
Theo đề bài, đồng hồ chạy đúng giờ nên T 1 = T 2 và △ T = 0
Suy ra 
STUDY TIP
Phải nắm vững tính chất của con lắc đơn khi chịu sự thay đổi về một trong các trạng thái như: thay đổi độ cao; nhiệt độ; chiều dài;… để áp dụng đúng công thức.
Chu kì dao động riêng của con lắc trong không khí và trong chân không được xác định bởi:
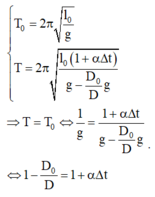
Thay các giá trị vào biểu thức, ta tìm được:
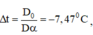
Vậy nhiệt độ của hộp chân không là 17,50 C.
Đáp án D
a)Gọi \(t_1\) là nhiệt độ đồng hồ chạy đúng.
Chu kì đồng hồ chạy đúng được xác định:
\(T_đ=T_1=2\pi\cdot\sqrt{\dfrac{l_1}{g_0}}=2\pi\cdot\sqrt{\dfrac{l_0\left(1+\alpha t_1\right)}{g_0}}\)
Khi nhiệt độ bằng \(10^oC\) thì chu kì đồng hồ chạy:
\(T_s=T_2=2\pi\cdot\sqrt{\dfrac{l_2}{g_0}}=2\pi\cdot\sqrt{\dfrac{l_0\cdot\left(1+\alpha t_2\right)}{g_0}}\)
Đồng hồ chạy nhanh 6,48 giây nên \(T_1>T_2\)
\(\Rightarrow t_1=\dfrac{2\cdot6,48}{\alpha t}+t_2=\dfrac{2\cdot6,48}{2\cdot10^{-5}\cdot24\cdot3600}+10=17,5s\)
b)Con lắc chịu sự biến đổi của sự nở dài về nhiệt và sự thay đổi độ cao.
\(\dfrac{\Delta T_1}{T_1}=\dfrac{1}{2}\alpha\left(t_2-t_1\right)+\dfrac{h}{R}\)
Đồng hồ chạy đúng giờ: \(T_1=T_2\) và \(\Delta T=0\)
\(\Rightarrow\dfrac{1}{2}\alpha\left(t_2-t_1\right)+\dfrac{h}{R}=0\)
\(\Rightarrow\dfrac{1}{2}\cdot2\cdot10^{-5}\cdot\left(6-10\right)+\dfrac{h}{6400}=0\)
\(\Rightarrow h=0,256km=256m\)
c)Chu kì dao động của con lắc để đồng hồ chạy đúng:
\(\left\{{}\begin{matrix}T=2\pi\sqrt{\dfrac{l_0}{g}}\\T'=2\pi\sqrt{\dfrac{l_0\cdot\left(1+\alpha\cdot\Delta t\right)}{g'}}\end{matrix}\right.\)
\(\Rightarrow T=T'\Rightarrow\dfrac{l_0}{g}=\dfrac{l_0\left(1+\alpha.\Delta t\right)}{g'}\)
Gia tốc vật rơi tự do: \(g'=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
\(\Rightarrow\dfrac{g'}{g}=\left(\dfrac{R}{R+h}\right)^2=1+\alpha.\Delta t\)
\(\Rightarrow\Delta t=\dfrac{\left(\dfrac{R}{R+h}\right)^2-1}{\alpha}=\dfrac{\left(\dfrac{6400}{6400+3,2}\right)^2-1}{2\cdot10^{-5}}\approx-50^oC=-58^oF\)
Chiều dài con lắc:
\(l=l_0\left(1+\alpha\Delta t\right)=3,2\cdot\left(1+2\cdot10^{-5}\cdot\left(-58\right)\right)=3,196288km\)
Chọn B
Chu kì của con lắc ở nhiệt độ t1 là T1 = 2 π l 1 g với l1 = l0(1+a.t1)
Chu kì của con lắc ở nhiệt độ t2 là T2 = 2 π l 2 g với l2 = l0(1+a.t2)
Lập tỷ lệ: T 2 T 1 = l 2 l 1 = 1 + α . t 2 1 + α . t 1 = 1 + α 2 . t 2 - α 2 . t 1 = 1 + α 2 . ( t 2 - t 1 ) (phép biến đổi có sử dụng công thức gần đúng)
+ Mỗi chu kỳ đồng hồ chỉ sai thời gian ΔT.
∆ T T 1 = T 2 - T 1 T 1 = 1 2 α ∆ t 0 ⇒ ∆ T = 1 2 T 1 α ∆ t 0
+ Do ΔT > 0 đồng hồ chạy chậm và mỗi ngày chậm:
ζ = n . ∆ T = 24 . 3600 T 1 . T 1 . α ∆ t 0 2 = 86400 . 2 . 10 - 5 ( 20 - 10 ) 2 = 8 , 64 ( s )