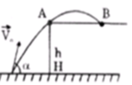
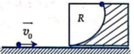
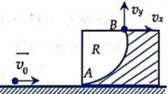
Em bé ngồi trên sàn nhà ném một viên bi lên bàn cao 1m với vận tốc v0 = 2 10 m/s. Để hòn bi có thể rơi xuống mặt bàn ở B cách xa mép bàn A nhất thì vec-tơ vận tốc v0 phải nghiêng với phương ngang một góc α bằng bao nhiêu ?
A. 450
B. 900
C. 600
D. 350

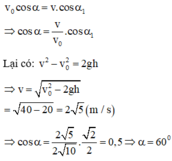
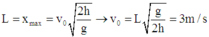
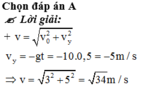


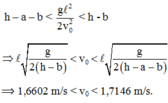
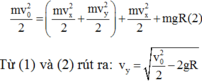
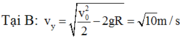
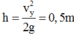
Đáp án: C
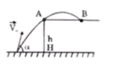
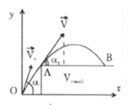
Để viên bi có thể rơi xa mép bàn A nhất thì quỹ đạo của viên bi phải sát A.
Gọi vận tốc viên bi tại A là v m/s.
Do theo phương Ox viên bi chuyển động đều nên các vận tốc thành phần bằng nhau:
Lại có: