Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và AB<CD.
M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).
AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E
1) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AQF luôn thuộc một đường thẳng cố định khi P di chuyển.

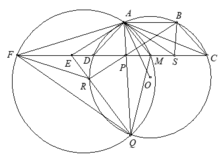
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.