Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố “Lấy lần thứ hai được một viên bi xanh”, ta được kết quả A. 5/8 B. 5/9 C. 5/7...
Đọc tiếp
Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố “Lấy lần thứ hai được một viên bi xanh”, ta được kết quả
A. 5/8
B. 5/9
C. 5/7
D. 4/7
Trường hợp 1: Lấy 3 viên bi cùng màu xanh ⇒ có 
cách chọn Trường hợp 2: Lấy 3 viên bi cùng màu đỏ ⇒ có 
cách chọn Trường hợp 3: Lấy 3 viên bi cùng màu vàng ⇒ có 
cách chọn Do đó suy ra 
.
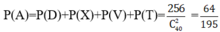
Gọi A là biến cố “Lấy lần thứ hai được một viên bi xanh”. Có hai trường hợp xảy ra
Biến cố B: Lấy lần thứ nhất được bi xanh, lấy lần thứ hai cũng được một bi xanh.
Xác suất trong trường hợp này là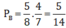
Biến cố C: Lấy lần thứ nhất được bi đỏ, lấy lần thứ hai được bi xanh.
Xác suất trong trường hợp này là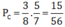
Ta thấy 2 biến cố B và C là xung khắc nên
→Đáp án A.