Một trường THPT có 25 em học sinh giỏi của 11A, 20 em học sinh giỏi ở 12A. Có bao nhiêu cách chọn 1 học sinh giỏi đi dự thi thực nghiệm ở trong lớp 11A; 12A
A: 45
B: 20
C: 35
D: 300
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
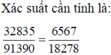


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
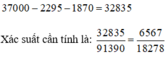
Chọn D

Chọn 3 học sinh lớp 12 có ![]() cách
cách
Chọn 1 học sinh lớp 11 có ![]() cách
cách
Chọn 1 học sinh lớp 10 có ![]() cách.
cách.
Do đó có ![]() cách chọn.
cách chọn.
Chọn B.

Cuối kì 1 thì :
Số học sinh giỏi bằng \(\frac{2}{7}\) số học sinh cả lớp nên số học sinh giỏi bằng \(\frac{2}{\left(2+7\right)}=\frac{2}{9}\)số học sinh cả lớp
Cuối năm thêm 1 học sinh nữa ta có :
Số học sinh giỏi bằng \(\frac{1}{3}\)số học sinh cả lớp nên số học sinh giỏi bằng \(\frac{1}{\left(1+3\right)}=\frac{1}{4}\)số học sinh cả lớp
Vậy 1 học sinh khá ứng với :
\(\frac{1}{4}-\frac{2}{9}=\frac{1}{36}\)( học sinh cả lớp )
Số học sinh cả lớp là :
\(1:\frac{1}{36}=36\)(học sinh)
Chúc bạn học tốt !!!

a: Số cách chọn là \(C^3_{18}=816\left(cách\right)\)
b: SỐ cách chọn là 7*6*5=210 cách
c: SỐ cách chọn là 7*5+5*6+7*6=107 cách
Đáp án : A
Phương án 1: Chọn 1 học sinh giỏi lớp 11A có 25 cách chọn.
Phương án 2: Chọn 1 học sinh giỏi lớp 12A có 20 cách chọn.
Theo quy tắc cộng; có 25+20=45 cách chọn.