Cho X={0;1;2;3;4;5;6;7}. Có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau từ X sao cho một trong 3 chữ số đầu tiên phải có mặt chữ số 1
A: 2280.
B. 840.
C.1440.
D. 2520.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
CM
26 tháng 10 2019
Đặt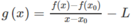 
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và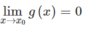 
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
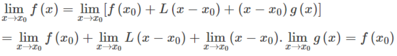
Vậy hàm số y = f(x) liên tục tại
CM
30 tháng 11 2017
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
TT
1
5 tháng 8 2017
Dễ thấy: \(x_0;y_0\ne 0\)
*)Xét \(x_0;y_0>0\) xài BĐT AM-GM
\(x^3+y^3+1\ge3\sqrt[3]{x^3y^3}=3xy\)
Xảy ra khi \(x=y=1\)
Khi đó \(\left(1+x_0\right)\left(1+\dfrac{1}{y_0}\right)\left(1+\dfrac{x_0}{y_0}\right)=8\)
*)Xét \(x_0;y_0<0\)\(\Rightarrow3xy>0;x^3+y^3+1\le0\) (loại)
CM
5 tháng 1 2017
- Định nghĩa:
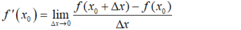
- Cho h = Δx, khi Δx → 0 thì h → 0 nên ta có:
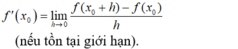
Chọn C
CM
24 tháng 7 2017
Ta có
x − y = 5 3 x + 2 y = 18 ⇔ x = y + 5 3. y + 5 + 2 y = 18 ⇔ x = y + 5 3 y + 15 + 2 y = 18 ⇔ x = y + 5 5 y = 3
⇔ y = 3 5 x = 5 + 3 5 ⇔ x = 28 5 y = 3 5
Vậy hệ phương trình có nghiệm duy nhất x ; y = 28 5 ; 3 5 ⇒ x . y = 84 25
Đáp án: B
Gọi số tự nhiên cần tìm có dạng
.
TH1: Nếu a=1 khi đó có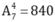
cách chọn 4 chữ số xếp vào b;c;d;e.
TH2: Nếu a khác 1 , khi đó: Có 6 cách chọn a. Có 2 cách xếp chữ số 1 vào số cần tạo ở vị trí b hoặc c. Các chữ số còn lại trong số cần tạo có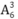
cách chọn.
Như vậy trường hợp này c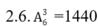ó
số.
Vậy có tất cả 840+1440=2280 số.
chọn A.