Một người đi xe máy từ A đến B với vận tốc 30 km/h. Lúc về người đó đi với vận tốc 24 km/h nên thời gian về nhiều hơn thời gian đi là 30 phút. Tính quãng đường AB?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 6 2019
đổi 45 phút = 34giờ
gọi x là quảng đường AB ( với x>0)
theo đề bài ta có:
x30−x40=34
⇒4x−3x=90
⇒x=90
vậy: SAB=90km
1 tháng 6 2019
Đổi 45 phút = 3/4 giờ
Gọi độ dài quãng đường AB là x ( km ) ( x > 0 )
Ta có thời gian lúc xe máy đi từ A đấn B là : x / 40 giờ
Thời gian lúc xe máy đi về là : x / 40 giờ
Theo bài ra ta có phương trình như sau :
x / 30 - 3 / 4 = x / 40 <=> 4x / 120 - 3x / 120 = 3 / 4 <=> x = 120 . 3 / 4 = 90 ( thỏa mãn điều kiện đê bài )
=> Quãng đường AB dài 90 km
~ Học tốt ~
26 tháng 3 2021
Gọi độ dài quãng đường AB là x(km)(Điều kiện: x>0)
Thời gian người đó đi từ A đến B là: \(\dfrac{x}{45}\left(h\right)\)
Thời gian người đó đi từ B về A là: \(\dfrac{x}{50}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{45}-\dfrac{x}{50}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{10x}{450}-\dfrac{9x}{450}=\dfrac{180}{450}\)
\(\Leftrightarrow x=180\left(nhận\right)\)
Vậy: Độ dài quãng đường AB là 180km
3 tháng 3 2022
Gọi độ dài quãng đường AB là x
Thời gian đi là x/40(h)
Thời gian về là x/35(h)
Theo đề, ta có: x/35-x/40=1/2
hay x=140
25 tháng 7 2021
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Theo đề, ta có phương trình:
\(\dfrac{x}{24}-\dfrac{x}{30}=\dfrac{1}{2}\)
\(\Leftrightarrow x\cdot\dfrac{1}{120}=\dfrac{1}{2}\)
hay \(x=\dfrac{1}{2}:\dfrac{1}{120}=\dfrac{1}{2}\cdot120=60\left(thỏa\right)\)
Vậy: Độ dài quãng đường AB là 60km
PD
30 tháng 3 2021
Gọi quãng đường AB là x (km, x>0)
Người đó đi xe đạp từ A đến B với vận tốc 15km/h
\(\to\) Thời gian lúc đi của người đó là \(\dfrac{x}{15}\) (h)
Người đó đi xe đạp từ B về A với vận tốc 12km/h
\(\to\) Thời gian lúc về của người đó là \(\dfrac{x}{12}\) (h)
Vì thời gian về nhiểu hơn thời gian đi là 30 phút
\(\to\) Ta có pt: \(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{30}{60}\)
\(\to 5x-4x=30\)
\(\to x=30\) (TM)
Vậy quãng đường AB là 30km
8 tháng 4 2022
Bạn tách ra nhá
Thôi, mình làm câu 1:
Vì thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch
V xuôi/V ngược = T ngược/T xuôi = 40/30 = 4/3
Ta có sơ đồ:
T xuôi: |-----|-----|-----| 30 phút
T ngược:|-----|-----|-----|-----|
T xuôi là:
30 : (4 - 3) x 3 = 90 phút = 1,5 giờ
Quãng đường là:
1,5 x 40 = 60km
Đ/s:..
G
8 tháng 4 2022
Vì quãng đường AB không đổi nên ta có :Đổi: \(45ph=\dfrac{3}{4}h\)
Gọi thời gian người đó đi từ A đến B là x (h) (x > 0)
Thời gian người đó từ B về A là
\(x-\dfrac{3}{4}\left(h\right)\)
Quãng đường người đó đi từ A đến B là 30x (km)
Quãng đường người đó đi từ A đến B là:
\(40.\left(x-\dfrac{3}{4}\right)=40x-30\left(km\right)\)
Vì quãng đường AB không đổi nên ta có :\(40x-30=30x\Leftrightarrow10x=30\Leftrightarrow x=3\left(h\right)\)Độ dài quãng đường AB là:
\(30.3=90\left(km\right)\)
29 tháng 6 2023
Gọi độ dài AB là x
Thời gian đi là x/30
Thời gian về là \(\dfrac{x+10}{25}\)
Theo đề, ta có: (x+10)/25-x/30=4/5
=>x/25-2/5-x/30=4/5
=>x/150=6/5
=>x=180
LL
29 tháng 6 2023
`->` gọi quãng đường `AB` là : `x(km;x>0)`
`-` quãng đường của xe máy lúc về là : `x+10(km)`
`-` thời gian của xe máy khi đi từ `A` đến `B` là : `x/30` (giờ)
`-` đổi `48` phút `=4/5` giờ
`=>` theo bài ra ta có được phương trình như sau :
`(x+10)/25-x/30=4/5`
`<=>6x -60+5x=120`
`<=>x=120-60`
`<=>x=60` (nhận)
Vậy quãng đường `AB` là `60km`
TT
5 tháng 5 2021
Gọi quãng đường AB là x(x>0)km
thời gian đi từ A đến B là \(\dfrac{x}{15}\)h
thời gian về từ B về A là \(\dfrac{x}{12}h\)
vì thời gian về lâu hơn thời gian đi là 30p =\(\dfrac{1}{2}\)h nên ta có pt
\(\dfrac{x}{12}\)-\(\dfrac{x}{15}\)=\(\dfrac{1}{2}\)
giải pt x=30 TM
vậy quãng đường AB dài 30 km
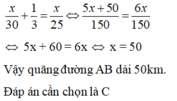
30 phút = (1/2) giờ
Gọi quãng đường AB là x (km). Điều kiện x > 0.
Thời gian xe máy đi từ A đến B là x/30 (giờ).
Thời gian xe máy đi từ B về A là x/24 (giờ).
Ta có phương trình:
⇔ 5x - 4x = 60 ⇔ x = 60 (thỏa mãn điều kiện)
Vậy quãng đường AB là 60 km.