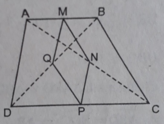
Bài 1 : Cho tứ giác ABCD , gọi M , N, P , Q theo thứ tự là trung điểm của AB , BC , CD , AD . Chứng minh rằng MNPQ là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

16 tháng 11 2021
Xét ΔADB có
M là trung điểm của AB
P là trung điểm của AD
Do đó: MP là đường trung bình của ΔADB
Suy ra: MP//BD và MP=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
Q là trung điểm của CD
Do đó: NQ là đường trung bình của ΔBCD
Suy ra: NQ//BD và NQ=BD/2(2)
Từ (1) và (2) suy ra MP//NQ và MP=NQ
hay MPQN là hình bình hành

6 tháng 1 2023
Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBDcó CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//PN và MQ=PN
=>MNPQ là hình bình hành

VB
22 tháng 12 2018
Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

CM
26 tháng 2 2017
MN // QP (cùng song song với BC)
MN = QP ( =1/2 BC)
⇒ MNPQ là hình bình hành.
Xét \(\Delta ABC\), có:
\(\left\{{}\begin{matrix}AM=MB\\AQ=QD\end{matrix}\right.\Rightarrow MQ\) là đường TB của \(\Delta ABC\)
\(\Rightarrow MQ\text{/}\text{/}=\dfrac{1}{2}BD\left(1\right)\)
Xét \(\Delta CBD\), có:
\(\left\{{}\begin{matrix}BN=NC\\CP=PD\end{matrix}\right.\Rightarrow NP\) là đường TB của \(\Delta CBD\)
\(\Rightarrow NP\text{/}\text{/}=\dfrac{1}{2}BD\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow NP\text{/}\text{/}MQ\)
Vậy...............