Phần tự luận
Nội dung câu hỏi 1
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O). Tiếp tuyến tại A của (O) cắt đường thẳng BC tại D. Gọi E là trung điểm của AD.
a) Chứng minh EC là tiếp tuyến của (O)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 7 2019
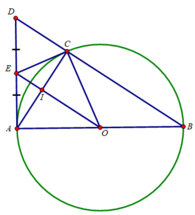
b) EA và EC là 2 tiếp tuyến của (O) cắt nhau tại E
⇒ EA = EC
Lại có: OA = OC
⇒ OE là đường trung trực của đoạn AC hay OE vuông góc với AC tại trung điểm I của AC
21 tháng 9 2021
a: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: ΔACD vuông tại C
mà CM là đường trung tuyến ứng với cạnh huyền AD
nên CM=MA
Xét ΔMAO và ΔMCO có
MA=MC
AO=CO
MO chung
Do đó: ΔMAO=ΔMCO
Suy ra: \(\widehat{MAO}=\widehat{MCO}\)
mà \(\widehat{MAO}=90^0\)
nên \(\widehat{MCO}=90^0\)
hay MC là tiếp tuyến của (O)
20 tháng 9 2021
b: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔABD có
O là trung điểm của AB
M là trung điểm của AD
Do đó: OM là đường trung bình của ΔABD
Suy ra: OM//BD
hay OM\(\perp\)AC
30 tháng 12 2023
a: Xét (O) có
MA,MC là các tiếp tuyến
Do đó: MA=MC
=>\(\widehat{MAC}=\widehat{MCA}\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)BD tại C
=>ΔACD vuông tại C
Ta có: \(\widehat{MDC}+\widehat{MAC}=90^0\)(ΔACD vuông tại C)
\(\widehat{MCD}+\widehat{MCA}=\widehat{DCA}=90^0\)
mà \(\widehat{MAC}=\widehat{MCA}\)
nên \(\widehat{MDC}=\widehat{MCD}\)
=>MC=MD
mà MC=MA
nên MA=MD
=>M là trung điểm của AD
b: Xét (O) có
MC,MA là các tiếp tuyến
Do đó: OM là phân giác của góc AOC
=>\(\widehat{AOC}=2\cdot\widehat{MOC}\)
Ta có: tia OC nằm giữa hai tia OM và ON
=>\(\widehat{MOC}+\widehat{NOC}=\widehat{MON}=90^0\)
=>\(\widehat{NOC}=90^0-\widehat{MOC}\)
Ta có: \(\widehat{COA}+\widehat{COB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{COM}+\widehat{COB}=2\cdot90^0=2\cdot\widehat{COM}+2\cdot\widehat{CON}\)
=>\(\widehat{COB}=2\cdot\widehat{CON}\)
=>ON là phân giác của góc COB
Xét ΔOBN và ΔOCN có
OB=OC
\(\widehat{BON}=\widehat{CON}\)
ON chung
Do đó: ΔOBN=ΔOCN
=>\(\widehat{OBN}=\widehat{OCN}=90^0\)
=>NB là tiếp tuyến của (O)
UI
26 tháng 2 2020
d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm
CM
14 tháng 3 2018
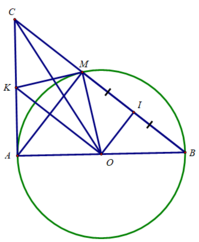
c) Tam giác CMA vuông tại M có MK là trung tuyến
⇒ MK = KA = KC
Xét Δ KAO và Δ KMO có:
KA = KM
KO là cạnh chung
AO = MO ( = bán kính (O))
⇒ Δ KAO = Δ KMO (c.c.c)
⇒ ∠(KAO) = ∠(KMO)
Mà ∠(KAO) = 90 0 ⇒ ∠(KMO) = 90 0
⇒ KM là tiếp tuyến của (O)
a) Ta có: ∠(ACB) = 90 0 (góc nội tiếp chắn nửa đường tròn)
⇒ AC ⊥ BD
ΔACD vuông tại C có CE là trung tuyến nên:
CE = EA = 1/2 AD
Xét ΔAEO và ΔCEO có:
AE = CE
EO : cạnh chung
AO = CO
⇒ ΔAEO = ΔCEO (c.c.c)
⇒ ∠(EAO) = ∠(ECO) = 90 0
⇒ CE là tiếp tuyến của (O)