Cho phương trình x + y = 1 (1). Phương trình nào sau đây có thể kết hợp với (1) để được một hệ phương trình bậc nhất hai ẩn có vô số nghiệm.
A.3x - 2y = 5
B. 3x + y = 1
C.x + 3y = 9
D.2x + 2y = 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 8 2019
Đáp án là B
x –2y = 2 ⇒ a = 1; b = -2; c = 2
A. 2x – 2y = 2 ⇒ a' = 2; b' = -2; c = 2
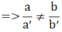⇒ hpt có 1 nghiệm duy nhất
B. -2x + 4y - 4 = 0 ⇔ -2x + 4y = 4 ⇒ a' = -2; b' = 4; c' = 4
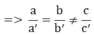⇒ hpt vô nghiệm
C. 2y = -2x – 4 ⇔ 2x + 2y = -4 ⇒ a' = 2; b'= 2; c' = -4
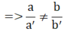⇒ hpt có 1 nghiệm duy nhất
D. y = 2x – 4 ⇔ -2x + y = -4 ⇒ a' = -2; b' = 1; c' = -4
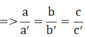⇒ hpt có vô số nghiệm
CM
18 tháng 6 2017
Chọn đáp án B.
x – y = 2 (1) ⇒ a = 1; b = -1; c = 2
A. 2x – 2y = 2 ⇒ a' = 2; b' = -2; c = 2
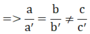⇒ hpt vô nghiệm
B. -2x + 2y + 4 = 0 ⇔ -2x + 2y = - 4 ⇒ a'= -2; b'= 2; c'= -4
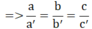⇒ hpt có vô số nghiệm
C. 2y = -2x – 4 ⇔ 2x + 2y = -4 ⇒ a' = 2; b' = 2; c' = -4
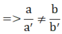⇒ hpt có 1 nghiệm duy nhất
D. y = 2x – 2 ⇔ 2x – y = 2 ⇒ a' = 2; b'= -1
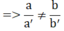⇒ hpt có 1 nghiệm duy nhất
6 tháng 10 2023
Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)
CM
30 tháng 11 2017
Ta có: 3x – 2y = 5 ⇔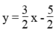 
Để được một hệ có vô số nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc bằng - 5/2 .
Chẳng hạn: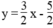 
⇔ 6x – 4y = 10
Khi đó ta có hệ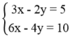 
có vô số nghiệm.
PT
1
CM
23 tháng 1 2018
Ta có: 3x – 2y = 5 ⇔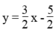 
Để được một hệ vô nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc khác - 5/2 .
Chẳng hạn: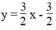 
⇔ 3x – 2y = 3
Khi đó ta có hệ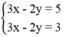 
vô nghiệm.
Đáp án là D