Trong tập hợp 4319 , 4321 , 4321 , 4322 , số nào chia hết cho cả 3 và 9
A. 4319
B. 4321
C. 4320
D. 4322
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 8 2017
Đúng(0)
Những câu hỏi liên quan
CC
10 tháng 6 2019
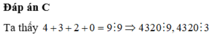
a) ta có \(\frac{1234}{1235}=1-\frac{1}{1235}\)
\(\frac{4319}{4320}=1-\frac{1}{4320}\)
vì \(\frac{1}{1235}>\frac{1}{4320}\Rightarrow1-\frac{1}{1235}< 1-\frac{1}{4320}\)
\(\Rightarrow\frac{1234}{1235}< \frac{4319}{4320}\)
b) ta có \(\frac{1234}{1244}=1-\frac{10}{1244}\)
\(\frac{4321}{4331}=1-\frac{10}{4331}\)
vì \(\frac{10}{1244}>\frac{10}{4331}\Rightarrow1-\frac{10}{1244}< 1-\frac{10}{4331}\)
\(\Rightarrow\frac{1234}{1244}< \frac{4321}{4331}\)
\(\Rightarrow\frac{-1234}{1244}>\frac{-4321}{4331}\)
29 tháng 6 2016
a) \(\frac{1}{1235}>\frac{1}{4320}\Rightarrow-\frac{1}{1235}< -\frac{1}{4320}\Rightarrow1-\frac{1}{1235}< 1-\frac{1}{4320}\Rightarrow\frac{1234}{1235}< \frac{4319}{4320}.\)
b) \(\frac{10}{1244}< \frac{10}{4331}\Rightarrow\frac{10}{1244}-1< \frac{10}{4331}-1\Rightarrow-\frac{1234}{1244}< -\frac{4321}{4331}\)
29 tháng 6 2016
a) Ta có:
1234/1235 = 1 - 1/1235
4319/4320 = 1 - 1/4320
Vì 1/1235 > 1/4320
=> 1234/1235 < 4319/4320
b) -1234/1244 = -1 + 10/1244
-4321/4331 = -1 + 10/4331
Vì 10/1244 > 10/4331
=> -1 + 10/4331 > -1/4331
Ủng hộ mk nha ♡_♡
15 tháng 12 2019
Từ abcd+abc+ab+a = 4321 (1) ta có:
1111a+11b+11c+d = 4321 (2)
- Từ (2) ta thấy a phải nhỏ hơn 4 vì nếu a=4 thì số hạng 1111a=4444 lớn hơn tổng của cả 4 số hạng nên không thể, nếu a=2 thì từ (1) ta thấy b+a \geq20 mà không có 2 số tự nhiên có 1 chữ số nào có tổng \geq20 nên cũng không thể, vậỵ a=3;
- Do a=3 nên ta có: 1111.3+111b+11c+d = 4321 hay 111b+11c+d = 4321-3333 = 988 (3)
Từ (3) ta thấy b phải nhỏ hơn 9 vì nếu b=9 thì số hạng 111b=999 lớn hơn tổng của cả 3 số hạng nên không thể; nếu a=7 thì từ (3) ta có 777+11c+d = 988 hay 11c+d = 211 (4), không thể tồn tại số tự nhiên c và d để thỏa mãn (4) nên b = 8;
- Do b=8 nên từ (3) có: 111.8+11c+d = 988 hay 11c+d = 100 (5)
Từ (5) ta thấy c không thể bằng 8 vì không tồn tại 88+d = 100 với d là số tự nhiên có 1 chữ số, do vậy c = 9;
- Do c = 9 nên từ (5) ta có d = 1.
Số các số cần tìm là: a = 3, b = 8, c = 9 và d = 1.
NV
1
4 tháng 10 2015
Cho (abcd) là số tự nhiên có 4 chữ số.
(abcd) + (abc) + (ab) + (a) = 1111.a + 111.b + 11.c + d
Vậy 1111.a + 111.b + 11.c + d = 4321
Nếu a < 3 => 111.b + 11.c + d > 2098 (khong hop ly vì b, c, d < 10)
Nếu a > 3 => vế trái > 4321
Vậy a = 3 => 111.b + 11.c + d = 988
Nếu b < 8 => 11.c + d > 210 (ko hop ly vì c, d < 10)
Nếu b > 8 => vế trái > 988
Vậy b = 8 => 11.c + d = 100
Nếu c < 9 => d > 11 (vô lý)
Vậy c = 9; d = 1 => (abcd) = 3891
HH
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
12 tháng 9 2023
a, 1ab+36 = ab1
=> 100 + 10a + b+36 = 100a+10b+1
<=> 100a - 10a + 10b -b = 100 + 36 - 1
<=> 90a+9b= 135
<=> 9(10a+b)= 135
<=>10a+b=135:9=15
Vì a,b khác 0 => a=1 và b=5 là thoả mãn
Vậy:a=1 và b=5