Dùng prôtôn bắn vào hạt nhân B 4 9 e đứng yên để gây phản ứng: p + B 4 9 e → X + L 3 6 i . Biết động năng của các hạt p, X, L 3 6 i lần lượt là 5,45MeV; 4,0MeV và 3,575MeV. Coi khối lượng các hạt tính theo u gần bằng số khối của nó. Góc hợp bởi hướng chuyển động của các hạt p và X gần đúng bằng:
A. 45 0
B. 120 0
C. 60 0
D. 90 0

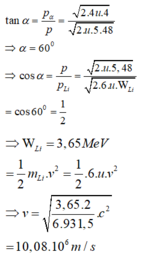
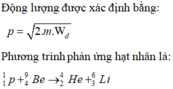
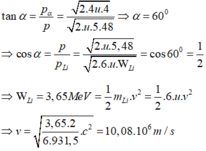
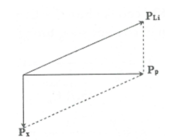

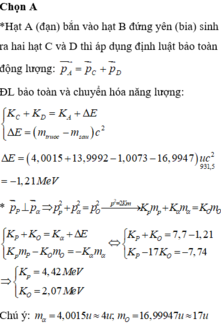
Đáp án D
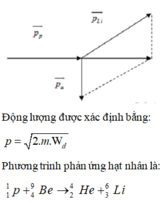
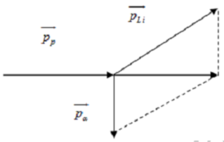
Theo định luật bảo toàn động lượng: