Tìm m để 3 đường thẳng sau đồng quy:
y = 2x - 1
y = (2m + 3)x - m + 1
y = x + 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai đường thẳng song song khi:
\(\left\{{}\begin{matrix}m^2-6=-2\\2m-1\ne m-3\end{matrix}\right.\) \(\Rightarrow m=2\)
Hai đường thẳng trùng nhau khi:
\(\left\{{}\begin{matrix}m^2-6=-2\\2m-1=m-3\end{matrix}\right.\) \(\Rightarrow m=-2\)

Tọa độ giao là:
-2x+4=x+1 và y=x+1
=>-3x=-3 và y=x+1
=>x=1 và y=2
Thay x=1 và y=2 vào y=3x+k, ta được:
k+3=2
=>k=-1

Ba đường thẳng đã cho đồng quy khi hệ 2 x + 3 y = 1 x - y = 2 m x + ( 2 m + 1 ) y = 2 có nghiệm duy nhất.
Xét hệ gồm hai phương trình (1) và (2) :
2 x + 3 y = 1 ( 1 ) x - y = 2 ( 2 ) ⇔ 2 x + 3 y = 1 2 x - 2 y = 4 ⇔ 2 x + 3 y = 1 5 y = - 3 ⇔ x = 7 5 y = - 3 5
Hệ này có nghiệm duy nhất là 7 5 ; - 3 5 .
Để ba đường thẳng đã cho đồng quy thì 7 5 ; - 3 5 cũng là nghiệm của phương trình (3), tức là
m . 7 5 + 2 m + 1 . - 3 5 = 2 ⇔ 7 m - 3 2 m + 1 = 10 ⇔ 7 m - 6 m - 3 = 10 ⇔ m = 13 .
Cho 2 đường thẳng
y = (m^2 - 3)x + m - 1
y = x + 1
Tìm m để 2 đường thẳng đó:
a. song song
b. trùng nhau

b: Để hai đường thẳng trùng nhau thì \(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m=2\end{matrix}\right.\Leftrightarrow m=2\)
Cho 2 đường thẳng
y = (m^2 - 3)x + m - 1
y = x + 1
Tìm m để 2 đường thẳng đó:
a. song song
b. trùng nhau

a: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m^2-3=1\\m-1\ne1\end{matrix}\right.\Leftrightarrow m=-2\)
b: Để hai đường thẳng trùng nhau thì \(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow m=2\)
Cho 2 đường thẳng
y = (m^2 - 3)x + m - 1
y = x + 1
Tìm m để 2 đường thẳng đó:
a. song song
b. trùng nhau

a, y = (m^2 - 3)x + m - 1 // y = x + 1
<=> \(\left\{{}\begin{matrix}m^2-3=1\\m-1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m\ne2\end{matrix}\right.\)
<=> m = \(\pm\)2 và \(m\ne2\)<=> m = -2
b, y = ( m^2 - 3 )x + m - 1 trùng y = x + 1
<=> \(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m=2\end{matrix}\right.\)<=> m = 2
a: Để hai đường thẳng song song thì
\(\left\{{}\begin{matrix}m^2-3=1\\m-1\ne1\end{matrix}\right.\Leftrightarrow m=-2\)
b: Để hai đường thẳng trùng nhau thì
\(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow m=2\)

a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 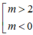
Kết luận 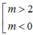
Gọi A là giao điểm của \(y=2x-1\) và \(y=x+2\)
Hoành độ A thỏa mãn:
\(2x-1=x+2\Rightarrow x=3\)
\(\Rightarrow y=5\)
\(\Rightarrow A\left(3;5\right)\)
3 đường thẳng đồng quy khi \(y=\left(2m+3\right)x-m+1\) đi qua A
\(\Rightarrow5=3\left(2m+3\right)-m+1\)
\(\Rightarrow m=-1\)