Cho hàm số y = x 2 − 2(m + 1 m )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là y 1 , y 2 thỏa mãn y 1 - y 2 = 8. Khi đó giá trị của m bằng
A. m = 1
B. m ∈ ∅
C. m = 2
D. m = 1, m = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\-2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne-3\end{matrix}\right.\)
kết hợp với điều kiện. Vậy m = 2
Tham Khảo:
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi
kết hợp với điều kiện. Vậy m = 2

Đặt y= f(x) = \(x^2-2\left(m+\dfrac{1}{m}\right)x+m\)
Hoành độ đỉnh của đồ thị hàm số x=\(m+\dfrac{1}{m}\ge2\) (BĐT co-si)
vì hệ số a =1>0 nên hàm số nghịch biến trên \(\left(-\infty;m+\dfrac{1}{m}\right)\)
Suy ra, hàm số nghịch biến trên \(\left[-1;1\right]\)
=> y1 = f(-1) = \(3m+\dfrac{2}{m}+1\)
y2 = f(1)=\(1-m-\dfrac{2}{m}\)
theo đề bài ta có : y1-y2=8 <=> \(3m+\dfrac{2}{m}+1-1+m+\dfrac{2}{m}=8\left(m>0\right)\)
<=> \(m^2-2m+1=0\)
<=> m=1

Khi x >0 thì hàm số nghịch biến khi 2015-m<0<=>m>2015

a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3


a: Thay x=-1 và y=-2 vào y=(m-1)x+2m, ta được:
\(-\left(m-1\right)+2m=-2\)
=>2m-m+1=-2
=>m+1=-2
=>m=-3
b: Khi m=-1 thì \(y=\left(-1-1\right)x+2\cdot\left(-1\right)=-2x-2\)
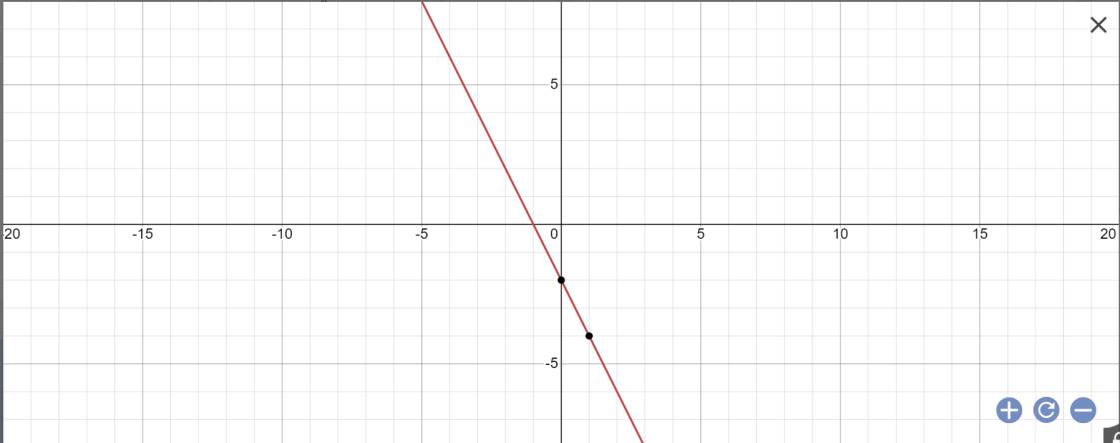
Đáp án A