Cho hình lập phương ABCD. A'B'C'D' cạnh a. Tính khoảng cách từ B tới đường thẳng DB'.
A. a 3 6
B. a 6 3
C. a 3 3
D. a 6 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

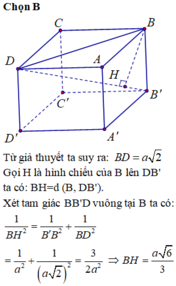

Đáp án A.
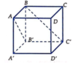
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3

Đáp án D.
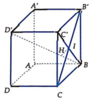
Cách 1: Gọi I là giao điểm của BC' và B'C . Trong B C ' D ' kẻ I H ⊥ B D ' tại H.
Ta có
B C ' ⊥ B ' C D ' C ' ⊥ B ' C B C ' , D ' C ' ∈ B C ' D ' ⇒ B ' C ⊥ B C ' D ' ⇒ B ' C ⊥ I H
Suy ra IH là đường vuông góc chung của BD' và B ' C ⇒ d B D ' , B ' C = I H .
Hai tam giác vuông BC'D' và BHI đồng dạng
⇒ I H D ' C ' = B I B D ' = a 2 2 a 3 = 6 6 ⇒ I H = a 6 6
Ta chọn D.
Cách 2: (Tọa độ hóa . Độc giả tự thực hiện)

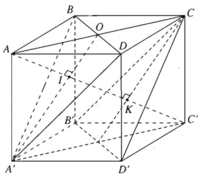
Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có:
C′B = C′D = C′A′ = a√2
Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.
Ta có A′I = BI = DI = 2A′O/3 với O là tâm của hình vuông ABCD
Ta lại có 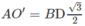
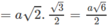
Vậy 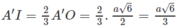
Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.

Điểm A cách đều ba đỉnh, của tam giác đều A'BD vì ta có AB = AD = AA' = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có :
\(C'B=C'D=C'A'=a\sqrt{2}\)
