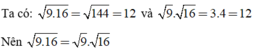So sánh 2 số 9 . 16 và 9 . 16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
2 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 7 2023
63 = (2.3)3 = 23.33 < 33.33 = 36
Vậy 36>63
162 = (24)2 = 28 < 29
Vậy 162 < 29
LT
0
NN
0
28 tháng 8 2015
19^20 và 9^8x5^16
Ta có 9^8.5^16
= (3^2)^8.5^16
=3^16.5^16
=15^16
Ta thấy 19^20 > 15^16
Do đó 19^20 > 9^8.5^16
17 tháng 2 2022
Ngoài đẹp hơn thì chẳng có gì cả
Còn lag hơn và bất tiện hơn
ML
2
KK
14 tháng 3 2019
Ta có: A = \(\frac{-2}{11}+\frac{6}{7}+\frac{1}{2}+\frac{-9}{11}+\frac{1}{7}\)
A = \(\left(\frac{-2}{11}+\frac{-9}{11}\right)+\left(\frac{6}{7}+\frac{1}{7}\right)+\frac{1}{2}\)
A = \(-1+1+\frac{1}{2}\)
A = \(\frac{1}{2}\)
B = \(\left(\frac{9}{16}+\frac{8}{27}\right)+\left(1+\frac{7}{16}+\frac{-19}{27}\right)\)
B = \(\frac{9}{16}+\frac{8}{27}+1+\frac{7}{16}-\frac{19}{27}\)
B = \(\left(\frac{9}{16}+\frac{7}{16}\right)+1+\left(\frac{8}{27}-\frac{19}{27}\right)\)
B = \(1+1-\frac{11}{27}\)
B = \(\frac{43}{27}\)
Mà 1/2 < 43/27 (Vì 1/2 < 1; 43/27 > 1)
=> A < B
KN
14 tháng 3 2019
Giải
\(A=\frac{-2}{11}+\frac{6}{7}+\frac{1}{2}+\frac{-9}{11}+\frac{1}{7}\)
\(\Leftrightarrow A=\left(\frac{-2}{11}+\frac{-9}{11}\right)+\left(\frac{6}{7}+\frac{1}{7}\right)+\frac{1}{2}\)
\(\Leftrightarrow A=\frac{-11}{11}+\frac{7}{7}+\frac{1}{2}\)
\(\Leftrightarrow A=-1+1+\frac{1}{2}\)
\(\Leftrightarrow A=\frac{1}{2}< 1\left(1\right)\)
\(B=\left(\frac{9}{16}+\frac{8}{27}\right)+\left(1+\frac{7}{16}+\frac{-19}{27}\right)\)
\(\Leftrightarrow B=\left(\frac{9}{16}+\frac{7}{16}\right)+\left(\frac{8}{27}+\frac{-19}{27}\right)+1\)
\(\Leftrightarrow B=\frac{16}{16}+\frac{-11}{27}+1\)
\(\Leftrightarrow B=1+\frac{-11}{27}+1\)
\(\Leftrightarrow B=2+\frac{-11}{27}\)
\(\Leftrightarrow B=\frac{43}{27}\)\(>1\left(2\right)\)
Từ (1) và (2) suy ra A < B