Tính giá trị biểu thức M = 2 3 - 1 4 + 2 - 2 - 5 2 + 1 4 - 5 2 - 1 3
A. 1 3
B. 3 2
C. 1 2
D. 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

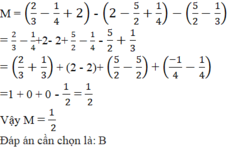

M=\(\frac{1}{1\cdot2}\)- \(\frac{1}{2\cdot3}\)+ \(\frac{1}{2\cdot3}\) - \(\frac{1}{3\cdot4}\) +..........+ \(\frac{1}{10\cdot11}\) - \(\frac{1}{11\cdot12}\)
= \(\frac{1}{2}\) - \(\frac{1}{11\cdot12}\)
=\(\frac{65}{132}\)

\(\dfrac{11}{2}\): \(\dfrac{1}{4}\) \(\times\) \(\dfrac{5}{3}\)
= \(\dfrac{11}{2}\) \(\times\) \(\dfrac{4}{1}\) \(\times\) \(\dfrac{5}{3}\)
= 22 \(\times\) \(\dfrac{5}{3}\)
= \(\dfrac{110}{3}\)
\(\dfrac{5}{2}-\dfrac{1}{4}+\dfrac{5}{3}\)
= \(\dfrac{30}{12}-\dfrac{3}{12}+\dfrac{20}{12}\)
= \(\dfrac{7}{12}\)
\(\dfrac{14}{5}\times\dfrac{2}{3}\)+ 5
= \(\dfrac{28}{15}\) + 5
= \(\dfrac{28}{15}\) + \(\dfrac{75}{15}\)
= \(\dfrac{103}{15}\)

\(\text{A}=1+\frac{3}{2^3}+\frac{4}{2^4}+\frac{5}{2^5}+...+\frac{100}{2^{100}}\)
\(\frac{1}{2}.\text{A}=\frac{1}{2}+\frac{3}{2^4}+\frac{4}{2^5}+...+\frac{99}{2^{100}}+\frac{100}{2^{101}}\)
\(=\left[\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{100}}\right]-\frac{100}{2^{101}}\left(\text{do}\frac{3}{2^3}=\frac{1}{2^2}+\frac{1}{2^3}\right)\)
\(=\frac{\left[1-\left(\frac{1}{2}\right)^{101}\right]}{\left(1-\frac{1}{2}\right)}-\frac{100}{2^{101}}\)
\(=\frac{\left(2^{101}-1\right)}{2^{100}}-\frac{100}{2^{101}}\)
\(\Rightarrow\text{A}=\frac{\left(2^{101}-1\right)}{2^{99}}-\frac{100}{2^{101}}\)
P/s: Sai đâu thì bn sửa nhé.

Bài 3 :
Vì \(\left(x-2\right)^2\ge0\forall x\)
Nên : \(A=\left(x-2\right)^2-4\ge-4\forall x\)
Vậy \(A_{min}=-4\) khi x = 2
B1: lấy máy tính mà tính thôi bạn (nhớ lm theo từng bước)
B2:
a, \(\left|x-\frac{2}{3}\right|-\frac{1}{2}=\frac{5}{6}\)
\(\left|x-\frac{2}{3}\right|=\frac{4}{3}\)
\(\Rightarrow\orbr{\begin{cases}x-\frac{2}{3}=\frac{4}{3}\\x-\frac{2}{3}=\frac{-4}{3}\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{-2}{3}\end{cases}}}\)
b, \(\frac{\left(-2\right)^x}{512}=-32\Rightarrow\left(-2\right)^x=-16384\Rightarrow x\in\varnothing\)
B3:
Vì \(\left(x-2\right)^2\ge0\Rightarrow A=\left(x-2\right)^2-4\ge-4\)
Dấu "=" xảy ra khi x = 2
Vậy GTNN của A = -4 khi x = 2

a)
\(\begin{array}{l}A = \left( {2 + \frac{1}{3} - \frac{2}{5}} \right) - \left( {7 - \frac{3}{5} - \frac{4}{3}} \right) - \left( {\frac{1}{5} + \frac{5}{3} - 4} \right).\\A = \left( {\frac{{30}}{{15}} + \frac{5}{{15}} - \frac{6}{{15}}} \right) - \left( {\frac{{105}}{{15}} - \frac{9}{{15}} - \frac{{20}}{{15}}} \right) - \left( {\frac{3}{{15}} + \frac{{25}}{{15}} - \frac{{60}}{{15}}} \right)\\A = \frac{{29}}{{15}} - \frac{{76}}{{15}} - \left( {\frac{{ - 32}}{{15}}} \right)\\A = \frac{{29}}{{15}} - \frac{{76}}{{15}} + \frac{{32}}{{15}}\\A = \frac{{ - 15}}{{15}}\\A = - 1\end{array}\)
b)
\(\begin{array}{l}A = \left( {2 + \frac{1}{3} - \frac{2}{5}} \right) - \left( {7 - \frac{3}{5} - \frac{4}{3}} \right) - \left( {\frac{1}{5} + \frac{5}{3} - 4} \right)\\A = 2 + \frac{1}{3} - \frac{2}{5} - 7 + \frac{3}{5} + \frac{4}{3} - \frac{1}{5} - \frac{5}{3} + 4\\A = \left( {2 - 7 + 4} \right) + \left( {\frac{1}{3} + \frac{4}{3} - \frac{5}{3}} \right) + \left( { - \frac{2}{5} + \frac{3}{5} - \frac{1}{5}} \right)\\A = - 1 + 0 + 0 = - 1\end{array}\)

M = 5 + 52 + 53 + 54 + ... + 559 + 560
5.M = 52 + 53 + 54 + 55 + ... + 560 + 561
5M - M =(52 + 53 + 54 + .... + 560 + 561) - (5 + 52 + 53 + ... + 559 + 560)
4M = 52 + 53 + 54 + .... + 560 + 561 - 5 - 52 - 53 - ...- 559 - 560
4M = (52 - 52) + (53 - 53) + ....+ (560 - 560) + (561 - 5)
4M = 561 - 5
4M + 5 = 561 - 5 + 5
4M = 561

Giải
M = 1/1+ 2 + 1/1 + 2+ 3 + 1/1 + 2+ 3+ 4 + 1/1 + 2+ 3+ 4+ 5 =
M= 1/3 + 1/6+1/10+1/15
M = 10/30 + 5/30 + 3/30 + 2/30
M= 20/30 =2/3
Làm như vậy đúng ko

Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)