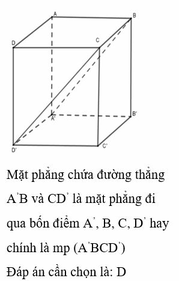
Cho hình hộp chữ nhật ABCD. A’B’C’D’. Gọi tên mặt phẳng chứa đường thẳng A’B và CD’. Hãy chọn câu đúng
A. mp (ABB’A’)
B. mp (ADD’A’)
C. mp (DCC’D’)
D. mp (A’BCD’)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


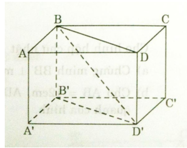
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)

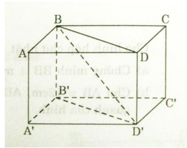
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)


a) BB’ ⊥ A’B’ (ABB’A’ là hình chữ nhật)
BB’ ⊥ B’C’ (BCC’B’ là hình chữ nhật)
=> BB’ ⊥ mp(A’B’C’D’)
=> BB’ ⊥ B’D’ hay
Hình bình hành BDD’B’ có một góc vuông nên là hình chữ nhật
BB’ vuông góc với hai đường thẳng cắt nhau AB và BC
=> BB’ ⊥ mp(ABCD)
c) mp(ABB’A’) chứa BB’ mà BB’⊥ mp(ABCD)
=> mp(ABB’A’) ⊥ mp(ABCD)

a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

a) Những đường thẳng song song với mặt phẳng (EFGH) là: AB; BC; CD; DA.
b) Đường thẳng AB song song với những mặt phẳng: (CDHG); (EFGH); (DCFE)
c) Đường thẳng AD song song với những đường thẳng: BC, FG, EH

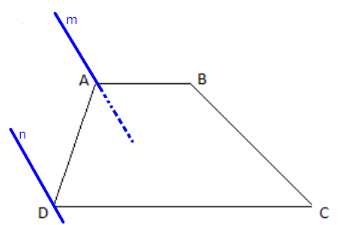
Ta có: m // n suy ra m // (C,n).
Có: AB // CD (do ABCD là hình thang) suy ra AB // (C,n).
Mặt phẳng (B,m) chứa hia đường thẳng cắt nhau m và AB song song với mp(C,n) suy ra (B,m) // (C,n).