Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Ta tách khối đa diện thành hai phần.
Phần 1. Lăng trụ tam giác DAF.CBE có V = 1 2
Phần 2. Hình chóp tam giác S.CEFD có
V S . C E F D = V B . C E F D = 2 3 V D A F . C B E = 1 3
⇒ V A B C D S E F = 5 6
Ta tách khối đa diện thành hai phần.
Phần 1. Lăng trụ tam giác DAF.CBE có V = 1 2
Phần 2. Hình chóp tam giác S.CEFD có
V S . C D F D = V B . C E F D = 2 3 V D A F . C B E = 1 3 ⇒ V A B C D E F = 5 6
Đáp án cần chọn là D
Đáp án D.
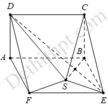
Vì S đối xứng với B qua
D E ⇒ d B ; D C E F = d S ; D C E E F .
Gọi M là trung điểm
C E ⇒ B M ⊥ D C E F ⇒ d B ; D C E F = B M .
Khi đó, thể tích V A B C D S E F = V A D F . B C E + V S . D C E F
= A B x S Δ A D F + 1 3 d S ; D C E F x S D C E F = 1. 1 2 + 1 3 . 2 2 . 2 = 1 2 + 1 3 = 5 6 .
Đáp án C