Gọi M, m lần lượt là GTLN, GTNN của hàm số y = x - 1 + 7 - x . Khi đó có bao nhiêu số nguyên nằm giữa m, M ?
A. 1
B. 2
C. Vô số
D. 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 3 2017
Chọn A.
Phương pháp: Sử dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất.
Vậy có 1 số nguyên dương là 3 nằm giữa M và m
CM
2 tháng 1 2020
Đáp án D
Ta có y ' = 1 − 1 x 2 ⇒ y ' = 0 ⇔ x = 1 x = − 1
Suy ra y 1 2 = 5 2 , y 1 = 2, y 3 = 10 3 ⇒ M = 10 3 m = 2 ⇒ M + m = 16 3
CM
28 tháng 10 2017
Chọn A.
Trên 1 2 ; 3 ta có: y ' = 1 - 1 x 2 ; y ' = 0 ⇔ x = 1 x = - 1 L
Khi đó y 1 2 = 5 2 , y 1 = 2 , y 3 = 10 3 . Vậy: 3 M + m = 12
TM
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
Đề là \(\dfrac{cos^2x}{3}+\dfrac{sinx}{3}+1\) hay \(cos^2\left(\dfrac{x}{3}\right)+sin\left(\dfrac{x}{3}\right)+1\) vậy nhỉ?
CM
4 tháng 11 2017
Đáp án B
Tập xác định: D = ℝ \ 1 2 ⇒ Hàm số y = m x + 1 2 x − 1 liên tục và đơn điệu trên 1 ; 3
⇒ a . b = y 1 . y 3 = m + 1 1 . 3 m + 1 5 = 1 5
⇔ m + 1 3 m + 1 = 1 ⇔ 3 m 2 + 4 m = 0 ⇔ m = 0 m = − 4 3
Vậy có 2 giá trị m thỏa mãn.
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)
Chọn A.
ĐK: 1 ≤ x ≤ 7
Ta có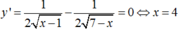
Xét y(1) = y(7) = 6 , y(4) = 2 3 suy ra 2,44 < k < 3,464 suy ra k = 3 có 1 số nguyên k.