P = 4a2+4ab+4b2-12a-12b+12 . Tính giÁ trị nhỏ nhất của P
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
AH
Akai Haruma
Giáo viên
14 tháng 9
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
AH
Akai Haruma
Giáo viên
14 tháng 9
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
21 tháng 3 2021
$P=4a^2+4a(b-3)+b^2-6b+9+3b^2-6b+3$
$=4a^2+2.2a.(b-3)+(b-3)^2+3.(b-1)^2$
$=(2a+b-3)^2+3.(b-1)^2$
Mà $(2a+b-3)^2 \geq 0;3.(b-1)^2 \geq 0$ với mọi $a;b$
Nên $P=(2a+b-3)^2+3.(b-1)^2 \geq 0$
Dấu $=$ xảy ra $⇔(2a+b-3)^2=0;3.(b-1)^2=0⇔2a+b-3=0;b=1⇔a=1;b=1$
Vậy $MinP=0$ tại $a=b=1$
HH
0
HN
7 tháng 3 2017
\(P=4a^2+4ab+4b^2+-12a-12b+12\)
\(=\left(\left(2a^2+4ab+2b^2\right)-8\left(a+b\right)+8\right)+\left(2a^2-4a+2\right)+\left(2b^2-4b+2\right)\)
\(=2\left(a+b-2\right)^2+2\left(a-1\right)^2+2\left(b-1\right)^2\ge0\)
Vậy GTNN của P = 0 khi x = y = 1
HN
20 tháng 2 2017
P = 4a2 + 4ab + 4b2 - 12a - 12b + 12
= [(4a2 - 12a + 9) + (4ab - 6b) + b2] + (3b2 - 6b + 3)
= [(2a - 3)2 + 2b(2a - 3) + b2] + 3(b - 1)2
= (2a + b - 3)2 + 3(b - 1)2\(\ge0\)
Dấu = xảy ra khi a = b = 1
CM
3 tháng 3 2017
Đáp án đúng : A
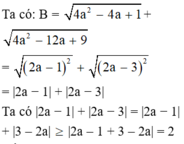
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2
A= 4a^2 + 4ab + 4b^2 - 12a - 12b + 12
=(2a+2b-3)^2 + 3
=>minA = 3
Ta có:
P=4a2+4ab+4b2-12a-12b+12
=[(4a2-12a+9)+2b(2a-3)+b2]+3b2-6b+12
=(2a+b-3)2+3(b-1)2+9
Dấu "=" xảy ra khi 2a+b-3=0 và b-1=0
<=>2a+1-3=0 và b=1
<=>a=1 và b=1
Vậy MinP=9 <=> a=b=1
Minh Lê Thái Bình xem lại cách giải nha :))))))))