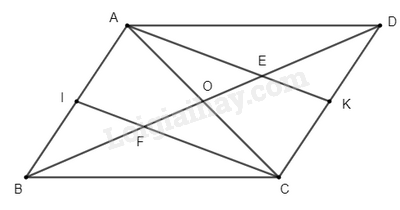
Cho hình bình hành ABCD. I, K lần lượt là trung điểm AB, CD.
a) Tứ giác AICK là hình gì?
b) AK, CI cắt BD tại E và F. Chứng mình: DE = EF = FB
c) Tứ giác EIFK là hình gì?
d) Chứng minh: AC, BD, IK đồng quy
e) Hình bình hành ABCD phải thỏa mãn điều kiện gì thì tam giác DIC cân tại I

Bài làm
a) Vì ABCD là hình bình hành
=> AB = DC (1)
Mà I là trung điểm AB => AI = IB = 1/2AB (2)
Và K là trung điểm AC => DK = KC = 1/2DC (3)
Từ (1), (2) và (3) => AI = IB = DK = KC
Vì AB // DC (vì ABCD là hình bình hành)
=> AI // KC
Xét tứ giác AICK có:
AI // KC (cmt)
AI = KC (cmt)
=> AICK là hình bình hành.
b) Xét tam giác DCF có:
KE // FC (Do AK // IC vì AICK là hình bình hành)
K là tủng điểm DC
=> KE là đường trung bình.
=> E là trung đểm DF
=> DE = EF (4)
Xét tam giác BAE có:
IF // AE (Vì AK // IF do AICK là hình bình hành)
I là trung điểm AB
=> IF là đường trung bình.
=> F là trung điểm EB
=> EF = FB (5)
Từ (4) và (5) => DE = EF = FB.
c) Vì AB // DC
=> \(\widehat{ABD}=\widehat{BDC}\)(so le trong)
Xét tam giác BIF và tam giác DKE có:
IB = DK (cmt)
\(\widehat{ABD}=\widehat{BDC}\)(cmt)
DE = FB (cmt)
=> Tam giác BIF = tam giác DKE (c.g.c)
=> IF = EK (hai cạnh tương ứng)
Xét tứ giác IFKC có:
IF = EK (cmt)
IF // EK (Do IC // AK)
=> IFKC là hình bình hành.
Còn câu d và e thì xin kiếu. Vì hình rối + câu cuối mình không biết làm ^^"