Cho tam giác ABC nhọn. M là 1 điểm bất kì trên BC. Kẻ MD vuông góc với AB, ME vuông góc với AC. Xác định vị trí điểm M trên BC để DE nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


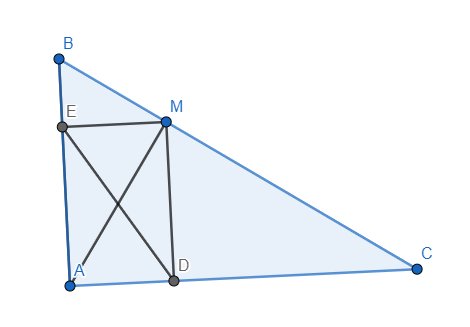
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC.

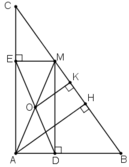
a) Tứ giác ADME có: 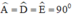
⇒ ADME là hình chữ nhật
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC.
Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH
⇒ OK là đường trung bình của ΔMAH
⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.

TH1: nếu tam giác ABC vuông tại A . bạn tự vẽ hình nhé
dễ thấy tứ giác ADME là hình chữ nhật .=> diện tích ADME=EM.MD
diện tích tam giác ABC=S=(AC.AB)/2
mặt khác ta có AC=AE+EC\(\ge\sqrt{AE\cdot EC}\)
\(AB=AD+DB\ge2\sqrt{AD\cdot DB}\)
==>\(AC\cdot AB\ge4\sqrt{AE\cdot EC\cdot AD\cdot DB}\)
ta có tam giác CEM đồng dạng tam giác MDB(g.g)=>\(\frac{CE}{MD}=\frac{EM}{DB}\)
=> CE.DB=EM.MD mà AE=MD ;AD=EM
do đó AE.EC.AD.DB=\(\left(EM\cdot MD\right)^2\)
=>2.diện tích ABC\(\ge\) diện tích tứ giác ADME==>diện tích ADME\(\le\frac{S}{2}\)
do đó MAX diện tích ADME=S/2 hay MAX diện tích MDE=S/4
dấu'=' xảy ra khi AE=EC và DA=DB hay M là trung điểm của BC
Gọi K là hình chiếu vuông góc của E lên MD, suy ra góc MEK = 90 - BAC.
Ta có 2 tam giác đồng dạng EDK và MAE
suy ra MA/DE = ME/EK = 1/sin(A)
suy ra DE nhỏ nhất khi MA nhỏ nhất
suy ra M là chân đường cao hạ từ A