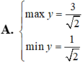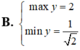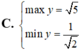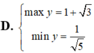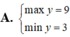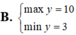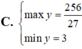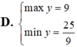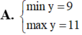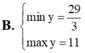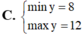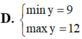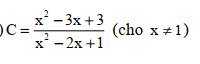tìm min hoặc max của 2x2+x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 7 2021
A = y^2 - 4y + 9 = y^2 - 4y + 4 + 5
= ( y - 2 )^2 + 5 >= 5
Dấu ''='' xảy ra khi y = 2
Vậy GTNN A là 5 khi y = 2
B = x^2 - x + 1 = x^2 - x + 1/4 + 3/4 = ( x - 1/2 )^2 + 3/4 >= 3/4
Dấu ''='' xảy ra khi x = 1/2
Vậy GTNN B là 3/4 khi x = 1/2
C = 2x^2 - 6x = 2 ( x^2 - 3x + 9 / 4 - 9/4 )
= 2 ( x - 3/2 )^2 - 9/2 >= -9/2
Dấu ''='' xảy ra khi x = 3/2
Vậy GTNN C là -9/2 khi x = 3/2
17 tháng 10 2021
\(D=\dfrac{21}{\left|x-2\right|+3}\le\dfrac{21}{3}=7\forall x\)
Dấu '=' xảy ra khi x=2
12 tháng 10 2020
Bài này tìm được min thôi
Ta có: \(2x^2+x=2\left(x^2+\frac{1}{2}x+\frac{1}{16}\right)-\frac{1}{8}=2\left(x+\frac{1}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(2\left(x+\frac{1}{4}\right)^2=0\Rightarrow x=-\frac{1}{4}\)
Vậy Min = -1/8 khi x = -1/4
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
\(A=\left|x-3\right|+\left|5-x\right|+\left|x+2\right|-4\ge\left|x-3\right|+\left|5-x+x+2\right|-4\)
\(A\ge\left|x-3\right|+3\ge3\)
\(A_{min}=3\) khi \(x=3\)
AH
Akai Haruma
Giáo viên
16 tháng 4 2023
Lời giải:
$C=\frac{x^2-3x+3}{x^2-2x+1}$
$\Rightarrow C(x^2-2x+1)=x^2-3x+3$
$\Leftrightarrow x^2(C-1)+x(3-2C)+(C-3)=0(*)$
Coi $(*)$ là pt bậc 2 ẩn $x$. Vì $C$ tồn tại nên $(*)$ có nghiệm.
$\Leftrightarrow \Delta'=(3-2C)^2-4(C-3)(C-1)\geq 0$
$\Leftrightarrow 4C-3\geq 0$
$\Leftrightarrow C\geq \frac{3}{4}$
Vậy $C_{\min}=\frac{3}{4}$
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1
Với mọi a;b ta có: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)
Áp dụng:
\(A=\left(x+3\right)^4+\left(7-x\right)^4\ge\dfrac{1}{2}\left[\left(x+3\right)^2+\left(7-x\right)^2\right]^2\)
Tiếp tục áp dụng BĐT ban đầu trong 2 số hạng trong ngoặc vuông:
\(\Rightarrow A\ge\dfrac{1}{2}\left[\dfrac{1}{2}\left(x+3+7-x\right)^2\right]^2=1250\)
Dấu "=" xảy ra khi \(x+3=7-x\Rightarrow x=2\)
Vậy \(A_{min}=1250\) khi \(x=2\)
Không tồn tại A max