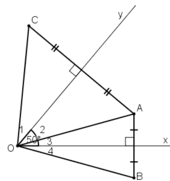
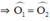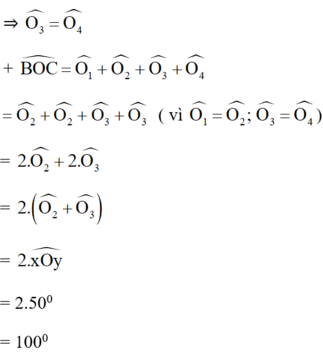bài 1 cho góc xOy nhọn, điểm A nằm trong góc đó vẽ điểm B đối xứng với A qua Ox, C đối xứng với A qua Oy. BC cắt các tia Ox; Oy theo thứ tự M; N. Chứng minh rằng trong các tam giác AM'N' (M' thuộc Ox; N' thuộc Oy; tam giác AMN có chu vi nhỏ nhất
HELP!!!!!!