Tập hợp các giá trị tự nhiên của n để phân thức (n4-2n3+5)/(n-2) có các giá trị nguyên là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
4 tháng 11 2019
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
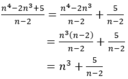
Vậy để N nguyên thì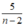 
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì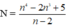 
có giá trị là số nguyên
AG
1
23 tháng 3 2017
Để A có giá trị nguyên thì
\(2n+5⋮n+1\)
\(\Rightarrow n+1⋮n+1\)
\(\Rightarrow2\left(n+1\right)⋮n+1\)
\(\Rightarrow2n+2⋮n+1\)
\(\Rightarrow\left[\left(2n+5\right)-\left(2n+2\right)\right]⋮n+1\)
\(\Rightarrow\left[2n+5-2n-2\right]⋮n+1\)
\(\Rightarrow3⋮n+1\)
\(\Rightarrow n+1\inƯ\left(3\right)\)
\(\Rightarrow n+1\in\left[1;3;-1;-3\right]\)
Xét \(n+1=1\Rightarrow n=0\)( thỏa mãn )
Xét \(n+1=3\Rightarrow n=2\)( thỏa mãn )
Xét \(n+1=-1\Rightarrow n=-2\)( loại vì n là số tự nhiên )
Xét \(n+1=-3\Rightarrow n=-4\)( loại vì n là số tự nhiên )
Vậy \(n\in\left[0;2\right]\)
12 tháng 11 2016
Giải:
Ta có: \(\frac{4}{n-1}+\frac{6}{n-1}-\frac{3}{n-1}=\frac{7}{n-1}\)
Mà \(\frac{4}{n-1}+\frac{6}{n-1}-\frac{3}{n-1}=\frac{7}{n-1}\in Z\)
\(\Rightarrow7⋮n-1\)
\(\Rightarrow n-1\in\left\{1;-1;7;-7\right\}\)
+) \(n-1=1\Rightarrow n=2\)
+) \(n-1=-1\Rightarrow n=0\)
+) \(n-1=7\Rightarrow n=8\)
+) \(n-1=-7\Rightarrow n=-6\)
Vậy \(n\in\left\{2;0;8;-6\right\}\)
PN
8 tháng 5 2016
a)Ta có ; để A thuộc N <=> (2n+5) chia hết cho (3n+1)
<=> 3(2n+5) chia hết cho (3n+1)
<=>(6n+15) chia hết cho (3n+1)
<=> (6n + 2 +13) chia hết cho (3n+1)
<=> 13 chia hết cho (3n+1)
=> (3n+1) thuộc Ư(13)
Vì n thuộc N
=> (3n+1) = 1,13
=> n = 0 hoặc 4
b)Trong phần này ta sẽ áp dung 1 tính chất sau:
a/b < (a+m)/(b+m) với a<b
Ta thấy :
x/(x+y) > x/(x+y+z)
y/(y+z) > y/(x+y+z)
z/(z+x) > z/(x+y+z)
=> A > x/(x+Y+z) + y/(x+y+z) + z/(x+y+z)
=> A>1
Ta thấy :
x/x+y < (x+z)/(x+y+z)
y/y+z < (y+x)/(x+y+z)
z/z+x < (z+y)/(x+y+z)
=> A < (x+z)/(x+y+z) +(y+x)/(x+y+z) +(z+y)/(x+y+z)
=>A< 2(x+y+z)/(x+y+z)
=> A<2
=>1<A<2
=> A ko phải là số nguyên(đpcm)
VT
4
\(\left(n^4-2n^3+5\right)=n^3\left(n-2\right)+5\) chia hết cho n -2
=> 5 chia hết cho n -2
n-2 thuộc U(5) = {1;5}
=> n thuộc { 3;7}
Vậy tập hợp có 2 phần tử