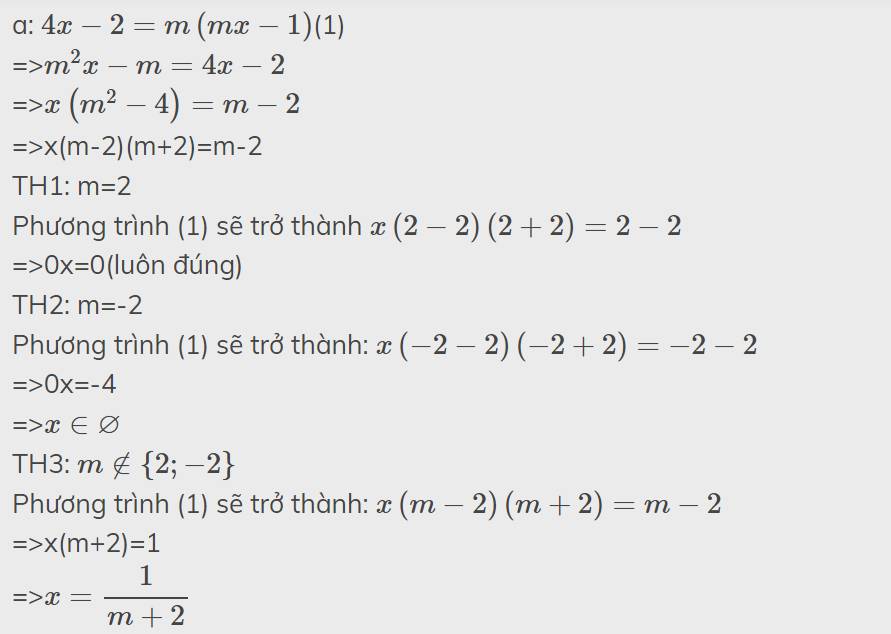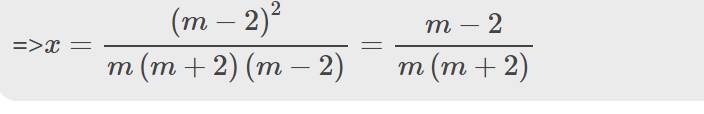Giải và biện luận bất phương trình : m2(mx-1)<m(1-m)x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
18 tháng 1 2019
m x - m 2 > 2 x - 4 ⇔ (m - 2)x > (m - 2)(m + 2)
Nếu m > 2 thì m – 2 > 0, bất phương trình có nghiệm là x > m + 2;
Nếu m < 2 thì m – 2 < 0, bất phương trình có nghiệm là x < m + 2;
Nếu m = 2 thì bất phương trình trở thành 0x > 0, bất phương trình vô nghiệm.
NT
0
T
1
30 tháng 12 2023
a: \(4x-2=m\left(mx-1\right)\)(1)
=>\(m^2x-m=4x-2\)
=>\(x\left(m^2-4\right)=m-2\)
=>x(m-2)(m+2)=m-2
TH1: m=2
Phương trình (1) sẽ trở thành \(x\left(2-2\right)\left(2+2\right)=2-2\)
=>0x=0(luôn đúng)
TH2: m=-2
Phương trình (1) sẽ trở thành: \(x\left(-2-2\right)\left(-2+2\right)=-2-2\)
=>0x=-4
=>\(x\in\varnothing\)
TH3: \(m\notin\left\{2;-2\right\}\)
Phương trình (1) sẽ trở thành: \(x\left(m-2\right)\left(m+2\right)=m-2\)
=>x(m+2)=1
=>\(x=\dfrac{1}{m+2}\)
f: \(m^2x-3=4x-\left(m-1\right)\)(2)
=>\(m^2x-4x=-m+1+3\)
=>\(x\left(m^2-4\right)=-m+2\)
=>\(x\left(m-2\right)\left(m+2\right)=-\left(m-2\right)\)
TH1: m=2
Phương trình (2) sẽ trở thành: \(x\left(2-2\right)\left(2+2\right)=-\left(2-2\right)\)
=>0x=0(luôn đúng)
TH2: m=-2
Phương trình (2) sẽ trở thành: \(x\left(-2-2\right)\left(-2+2\right)=-\left(-2-2\right)\)
=>0x=4
=>\(x\in\varnothing\)
TH3: \(m\notin\left\{2;-2\right\}\)
Phương trình (2) sẽ là: x(m-2)(m+2)=-(m-2)
=>x(m+2)=-1
=>\(x=-\dfrac{1}{m+2}\)
g: \(m^3x-4=m^2+4mx-4m\)(3)
=>\(m^3x-4mx=m^2-4m+4\)
=>\(x\left(m^3-4m\right)=\left(m-2\right)^2\)
=>\(x\cdot m\cdot\left(m+2\right)\left(m-2\right)=\left(m-2\right)^2\)
TH1: m=2
Phương trình (3) sẽ trở thành: \(x\cdot2\cdot\left(2+2\right)\left(2-2\right)=\left(2-2\right)^2\)
=>0x=0(luôn đúng)
TH2: m=0
Phương trình (3) sẽ trở thành:
\(x\cdot0\cdot\left(0+2\right)\left(0-2\right)=\left(0-2\right)^2\)
=>0x=4
=>\(x\in\varnothing\)
TH3: m=-2
Phương trình (3) sẽ trở thành;
\(x\cdot\left(-2\right)\left(-2+2\right)\left(-2-2\right)=\left(-2-2\right)^2\)
=>0x=16
=>\(x\in\varnothing\)
TH4: \(m\notin\left\{0;2;-2\right\}\)
Phương trình (3) sẽ trở thành:
\(x\cdot m\left(m+2\right)\left(m-2\right)=\left(m-2\right)^2\)
=>\(x=\dfrac{\left(m-2\right)^2}{m\left(m+2\right)\left(m-2\right)}=\dfrac{m-2}{m\left(m+2\right)}\)
G
3
25 tháng 2 2016
\(mx^2+\left(m+1\right)x-2m\le0\) (1)
Nếu \(m=0\) thì dễ thấy (1) có nghiệm \(x\le0\)
Xét \(m\ne0\) Khi đó (1) là bất phương trình bậc hai với a=m.
Ngoài ra, biệt thức
\(\Delta=9m^2+2m+1=\left(3m+\frac{1}{3}\right)^2+\frac{8}{9}>0\) \(\curlyvee m\in R\). Từ đó ta có ngay kết luận :
- Khi m < 0, bất phương trình (1) có tập nghiệm
T(1) = \(\left(x;\frac{-m-1+\sqrt{9m^2+2m+1}}{2m}\right)\)\(\cup\)\(\left(\frac{-m-1-\sqrt{9m^2+2m+1}}{2m};+\infty\right)\)
- Khi m = 0, bất phương trình (1) có tập nghiệm T(1) =R+
- Khi m>0, bất phương trình (1) có tập nghiệm
T(1)=\(\left(\frac{-m-1-\sqrt{9m^2+2m+1}}{2m};\frac{-m-1+\sqrt{9m^2+2m+1}}{2m}\right)\)
LM
0
VD
0
MN
16 tháng 1 2021
\(\left(x+1\right)\left(mx-3\right)=0\)
\(TC:\)
\(\left(+\right)x+1=0\Leftrightarrow x=-1\)
\(\left(+\right)mx-3=0\left(1\right)\)
\(BL:\)
\(\left(-\right)Với:m=0\\ \left(1\right)\Leftrightarrow0x-3=0\\ \Rightarrow PTVN\)
\(\left(-\right)Với:m\ne0\\ \left(1\right)\Leftrightarrow mx-3=0\\ \Leftrightarrow x=\dfrac{3}{m}\)
16 tháng 1 2021
có: \(\left(x+1\right).\left(mx-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\mx-3=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0-1=-1\\mx=0+3=3\end{matrix}\right.\)
Có x= -1 nên mx = (-3).(-1) => m= -3
Vậy x=-1 và m = -3