Cho hình thang ABCD (AB//CD), AB = 1/2CD. H là trung điểm của CD. Trên nửa mặt phẳng bờ CD không chứa A kẻ MH vuông góc với CD và MH = 1/4CD. Bên ngoài hình thang ABCD vẽ tam giác ADE vuông cân tại E và tam giác BCF vuông tại F. Chứng minh tam giác EMF vuông cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CB
8 tháng 6 2018
Câu 1:
Gọi mỗi đinh của tứ giác là A, B, C, D. Các góc ngoài tương ứng lần lượt là A1, B1, C1, D1
Ta có: A+ B+ C+ D+ A1+ B1+ C1+ D1= 720 độ
Ma A+ B+ C+ D= 360 độ nên A1+ B1+ C1+ D1= 720 - 360= 360 độ
LD
5 tháng 9 2017
Bài 1:
Gọi N là trung điểm của HC
Xét tam giác ABC cân tại A ta có:
AM là đường trung tuyến (gt)
=> AM là đường cao của tam giác ABC
=> AM _|_ BC tại M
Xét tam giác HMC ta có:
O là trung điểm của Mh (gt)
N là trung điểm của HC ( cách vẽ)
=> ON là đường trung bình của tam giác HMC
=> ON // MC
Mà AM _|_ MC tại M (cmt)
Nên NO _|_ AM
Mặt khác MH _|_ AN tại H (gt) và NO cắt MH tại O (gt)
=> O là trực tâm của tam giác AMN
=> AO _|_ MN
Xét tam giác BHC ta có:
M là trung điểm của BC (gt)
N là trung điểm của HC (cách vẽ)
=> MN là đường trung bình của tam giác BHC
=> MN // BH
Mà AO _|_ MN (cmt)
Nên AO _|_ BH (đpcm)
29 tháng 4 2018
LLớp 8 chúng tôi mới lớp #4 hóm này njpnnvidynnw này là chử viết gìn dayenws
CM
15 tháng 3 2017
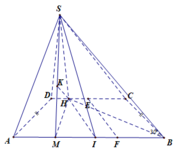
Đáp án D
Gọi M, E là trung điểm của AI và CD
Kẻ S H ⊥ C D do mặt phẳng (SCD) vuông góc với mặt phẳng
(ABCD) nên S H ⊥ ( A B C D ) . Mặt khác SA=SI
⇒ S M ⊥ A I ⇒ A I ⊥ ( S H M ) ⇒ H K ⊥ ( S A I ) mà CD
Song song với (SAB) ⇒ H K là khoảng cách cần tìm.
Qua E kẻ đường thẳng song song với BC cắt AB tại F
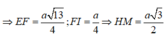
⇒ H B = a 3 ; S H = H B . tan 30 o = a 3 . 1 3 = a
Ta có 1 H K 2 = 1 S H 2 + 1 H M 2 = 1 a 2 + 4 3 a 2 = 7 3 a 2
⇒ H K = a 21 7
CM
15 tháng 8 2019
Gọi M; E là trung điểm của AI và CD
Kẻ S H ⊥ C D do mặt phẳng (SCD) vuông góc với mặt phẳng(ABCD) nên S H ⊥ A B C D . Mặt khác SA = SI
⇒ S M ⊥ A I ⇒ A I ⊥ S H M ⇒ H K ⊥ S A I
mà CD . Song song với S A B ⇒ H K là khoảng cách cần tìm. Qua E kẻ đường thẳng song song với BC cắt AB tại F
⇒ E F = a 13 4 ; F I = a 4 ⇒ H M = a 3 2 ⇒ H B = a 3 S H = H B . tan 30 o = a 3 . 1 3 = a
Ta có
1 H K 2 = 1 S H 2 + 1 H M 2 = 1 a 2 + 4 3 a 2 = 7 3 a 2 ⇒ H K = a 21 7
Đáp án cần chọn là D