Cho hai tam giác ABC và A'B'C' có trọng tâm tương ứng là G và G'.
Chứng mình rằng: véctơ AA' + véctơ BB'= véctơ CC' + vecto DD'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 8 2018
Xét hai tam giác ABC và tam giác MNP có A ^ = M ^ , B ^ = N ^ .
Để hai tam giác ABC và MNP bằng nhau cần điều kiện A B = M N theo trường hợp góc – cạnh – góc .
Chọn đáp án B.
17 tháng 9 2023
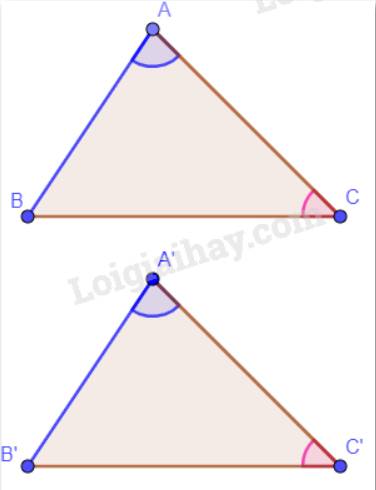
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
16 tháng 3 2022
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
Bạn coi lại đề, 2 điểm D và D' là điểm nào nhỉ?