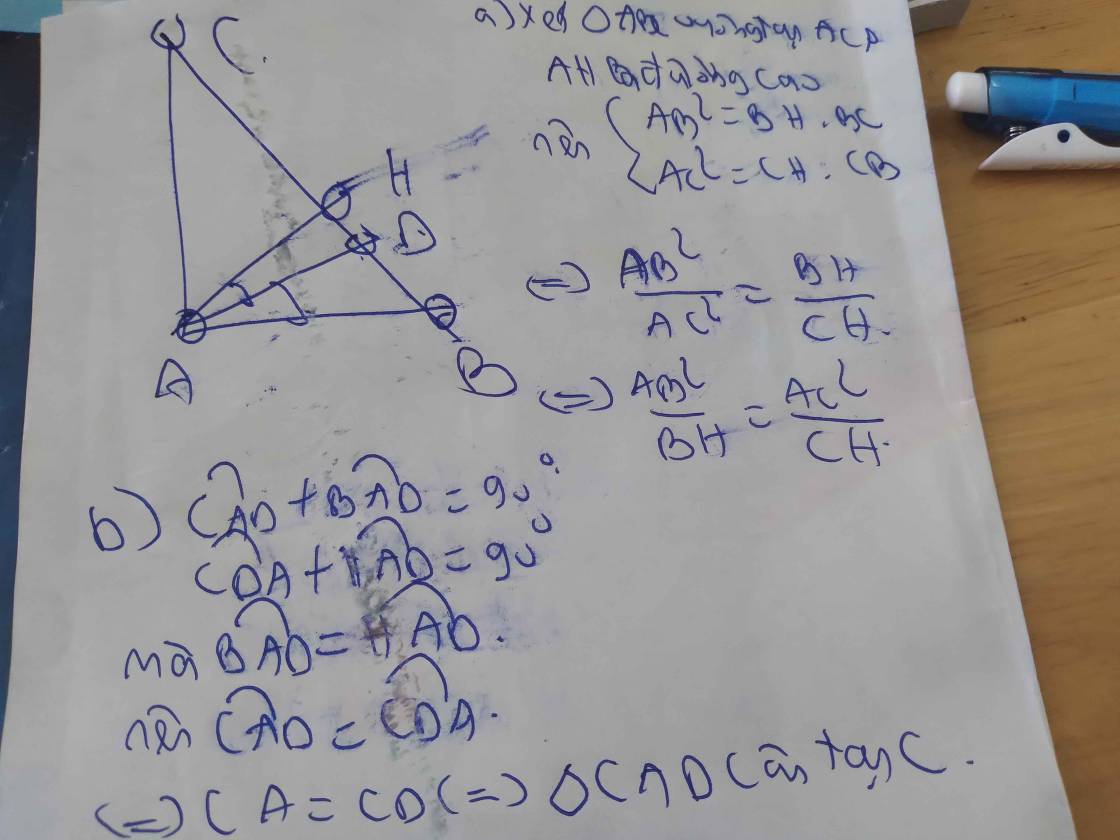Cho Tam Giác ABC vuông tại A, AB > AC, kẻ đường cao AH
a)Chứng minh \(\frac{AB^2}{BH}=\frac{AC^2}{CH}\)
b) Kẻ AD tia phân giác góc BAH. C/m tam giác ACD cân và DH.DC = BD.HC
c) Tính AH nếu cho biếu S ABH = 15,36 \(cm^2\); S ACH = 8,64 \(cm^2\)
d) Gọi M là trung điểm của AB, F là giao của 2 đường thẳng MD và AH. C/m CF//AD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

4 tháng 11 2021
a: BC=13cm
\(AB=3\sqrt{13}\left(cm\right)\)
\(AC=2\sqrt{13}\left(cm\right)\)

16 tháng 4 2022
a: Xét ΔABC có AB<AC
mà BH là hình chiếu của AB trên BC
và CH là hình chiếu của AC trên BC
nên HB<HC
Ta có:AB<AC
nên \(\widehat{B}>\widehat{C}\)
hay \(\widehat{BAH}< \widehat{CAH}\)
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)
mà \(\widehat{CAD}=\widehat{HAD}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
hay ΔBDA cân tại B