Một vật chuyển động thẳng nhanh dần đều với vận tốc ban đầu v0 =5 m /s , gia tốc a= 2m/s^2 . Tại thời điểm t vật đi được quãng đường 50m, vận tốc của vật trước thời điểm đó 1s là A. 15m/s B. 12m/s C. 13m/s D. 17m/s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn chiều dương là chiều chuyển động, gốc tọa độ trùng với vị trí ban đầu của vật, gốc thời gian là xuất phát.
a) Phương trình vận tốc: v = 6 + 4 t (m/s).
Đồ thị vận tốc - thời gian được biểu diễn như hình 12.
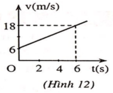
b) Khi v = 18 m/s thì t = 18 − 6 4 = 3 s.
Từ công thức v 2 − v 0 2 = 2 a s
quãng đường s = v 2 − v 0 2 2 a = 18 2 − 6 2 2.4 = 36 m.
c) Phương trình chuyển động: x = 6 t + 2 t 2 (m).
Khi v = 12 m/s thì t = 12 − 6 4 = 1 , 5 s ⇒ tọa độ x = 6.1 , 5 + 2.1 , 5 2 = 13 , 5 m.

a. Áp dụng công thức: \(S=v_0t+\dfrac{1}{2}at^2\)
\(\Rightarrow 1=2.t+0,25t^2\)
\(\Rightarrow 0,25 t^2+2t-1=0\)
Giải pt tìm được \(t\approx 0,47s\)
b, Để tìm thời gian vật đi hết 1m cuối cùng, ta tìm thời gian vật đi trong 45m trừ đi thời gian vật đi hết 44 m. Cách tìm thời gian từng đoạn này giống ý a, bạn tự làm nhé :)

a/ Ta có :
\(x=10+5t-8t^2\)
Có phương trình chuyển động dạng TQ : \(x=x_o+v_ot+\dfrac{1}{2}at^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-4m\backslash s^2\\v_o=5m\backslash s\end{matrix}\right.\)
b/ \(t=1s\)
\(v=v_o+at=5-4.1=1m\backslash s\)
c/ \(v^2-v_o^2=2as\)
\(\Leftrightarrow s=\dfrac{-v_o^2}{2a}=\dfrac{-5^2}{2.\left(-4\right)}=3,125\left(m\right)\)

Chọn A.
Vận tốc vật:
\(v^2-v^2_0=2aS\Rightarrow v=\sqrt{2aS+v_0^2}=\sqrt{2\cdot2\cdot50+5^2}=15\)m/s