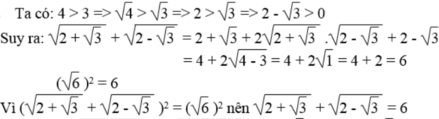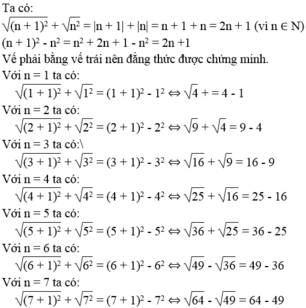Chứng minh đẳng thức:√(2+√3)=√6+√2/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
5
NX
1
3 tháng 7 2017
VT = \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\dfrac{\sqrt{4+2\sqrt{3}}}{\sqrt{2}}+\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}+1\right)^2}}{\sqrt{2}}+\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}=\dfrac{\sqrt{3}+1}{\sqrt{2}}+\dfrac{\sqrt{3}-1}{\sqrt{2}}\)
\(=\dfrac{\sqrt{3}+1+\sqrt{3}-1}{\sqrt{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{2}\left(\sqrt{6}\right)}{\sqrt{2}}=\sqrt{6}\) = VP (đpcm)
AH
6 tháng 7 2018
Để câu trả lời của bạn nhanh chóng được duyệt và hiển thị, hãy gửi câu trả lời đầy đủ và không nên:
- Yêu cầu, gợi ý các bạn khác chọn (k) đúng cho mình
- Chỉ ghi đáp số mà không có lời giải, hoặc nội dung không liên quan đến câu hỏi.
19 tháng 8 2021
a: Ta có: \(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}}{2}-\dfrac{4\sqrt{6}}{2}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{-3}{2}\)
7 tháng 7 2021
\(=\left(\dfrac{\sqrt{10}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}-\dfrac{\sqrt{6^2}}{\sqrt{6}}\right)\sqrt{4+\sqrt{15}}\)
\(=\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)\sqrt{4+\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{5+2\sqrt{3}\sqrt{5}+3}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
RK
7 tháng 7 2021
\(VT\Leftrightarrow\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8+2\sqrt{15}}=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2=VP\left(dpcm\right)\)
HS
3
NL
2 tháng 10 2018
Đặt VT = A =
=> \(A\sqrt{2}\) = \(\sqrt{2}\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)\)
= \(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\) = \(\sqrt{3+2\sqrt{3}+1}+\sqrt{3-2\sqrt{3}+1}\)
= \(\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\) = \(\sqrt{3}+1+\sqrt{3}-1=2\sqrt{3}\)
VP = B => \(B\sqrt{2}=\sqrt{2}.\sqrt{6}=2\sqrt{3}\)
=> \(A\sqrt{2}=B\sqrt{2}\Rightarrow A=B\)
2 tháng 10 2018
\(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\sqrt{6}\)
<=> \(\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2\)= \(6\)
* Xét vế trái ta có :
\(\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2\)
= \(\left(\sqrt{2+\sqrt{3}}\right)^2+2\left(\sqrt{2+\sqrt{3}}\right)\left(\sqrt{2-\sqrt{3}}\right)+\left(\sqrt{2-\sqrt{3}}\right)^2\)
= \(2+\sqrt{3}+2\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)+2-\sqrt{3}\)
=
