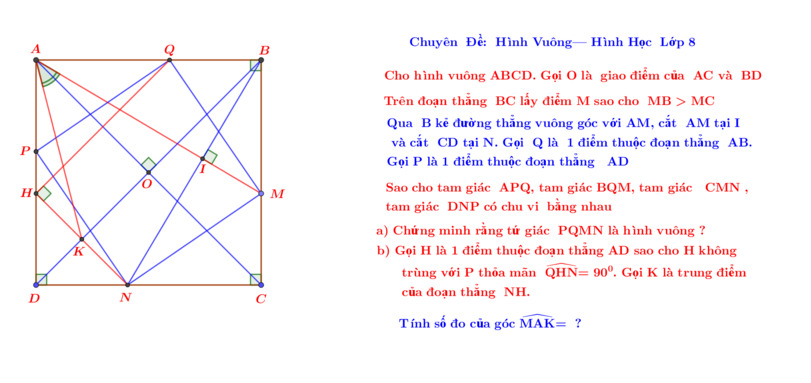
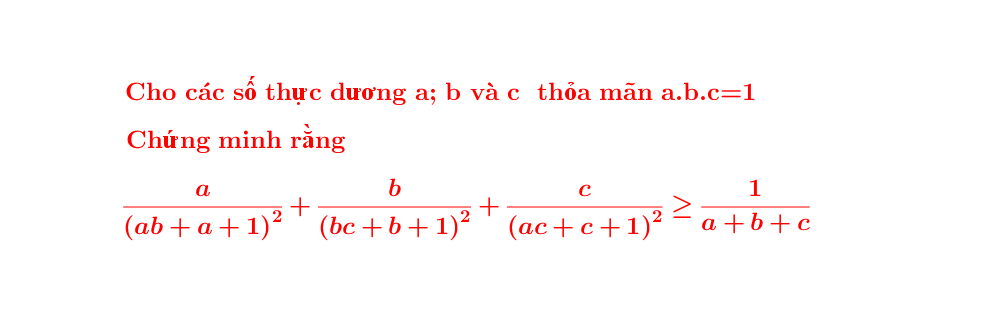Xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PK
0
Những câu hỏi liên quan
PK
2
13 tháng 2 2022
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
PK
0
PK
0
XO
5 tháng 4 2022
Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2022
Đặt \(a=p^q+7q^p\)
Nếu p; q đều bằng 2 \(\Rightarrow a=2^2+7.2^2\) là hợp số (ktm)
Nếu p; q cùng lớn hơn 2 \(\Rightarrow p^q\) và \(q^p\) đều lẻ
\(\Rightarrow a=p^q+7q^p\) là số chẵn lớn hơn 2 \(\Rightarrow\) là hợp số (ktm)
\(\Rightarrow\) Có đúng 1 số trong p; q phải bằng 2, số còn lại là SNT lẻ
TH1: \(p=2\Rightarrow a=2^q+7.q^2\)
- Nếu \(q=3\Rightarrow a=2^3+7.3^2=71\) là SNT (thỏa mãn)
- Nếu \(q>3\Rightarrow q^2\equiv1\left(mod3\right)\Rightarrow7q^2\equiv1\left(mod3\right)\)
\(2^q=2^{2k+1}=2.4^k\equiv2\left(mod3\right)\)
\(\Rightarrow a=2^q+7.q^2\equiv2+1\left(mod3\right)\Rightarrow a⋮3\) là hợp số (ktm)
TH2: \(q=2\Rightarrow a=p^2+7.2^p\)
- Nếu \(p=3\Rightarrow a=3^2+7.2^3=65\) ko phải SNT (ktm)
- Nếu \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(7.2^p=7.2^{2k+1}=14.4^k\equiv2\left(mod3\right)\)
\(\Rightarrow p^2+7.2^p⋮3\) là hợp số (ktm)
Vậy \(\left(p;q\right)=\left(2;3\right)\) là cặp SNT duy nhất thỏa mãn yêu cầu
6 tháng 4 2022
Đây là bài toán rất khó về đồng dư thức, em cám ơn thầy Lâm đã giải rất cẩn thận ạ!
25 tháng 2 2022
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{A}\) chung
Do đó: ΔAEB∼ΔAFC
Suy ra: AE/AF=AB/AC
hay AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
Do đó: ΔAEF∼ΔABC
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)
19 tháng 4 2022
Xét p=2\(\Rightarrow p^4+29=45=3^2.5\), có 6 ước số là SND, loại
Xét p=3\(\Rightarrow p^4+29=110=2.5.11\), có 8 ước số là SND, tm
Xét p=5\(\Rightarrow p^4+29=654=2.3.109\) , có 8 ước số là SND, tm
Xét p\(\ge6\). Do p là SNT nên p có dạng \(6k+1\) hoặc \(6k-1\) (k\(\in N\)*)
TH1: p=6k+1
Khi đó ta có \(p^4+29=\left(6k+1\right)^4+29\equiv1+29\equiv0\left(mod6\right)\)
Ta cũng có: \(p^4+29=\left(6k+1\right)^4+29\equiv0\left(mod5\right)\)
vì \(\left(6k+1\right)⋮5̸\)
\(\Rightarrow p^4+29=6.5.a=2.3.5.a\)(a là STN)\(\Rightarrow p^4+29\) có nhiều hơn 8 ước số nguyên dương, loại.
TH2: p=6k-1. Chứng minh tương tự ta thấy không có p thoả mãn
\(\Rightarrow p\ge6\) không thoả mãn
Vậy....