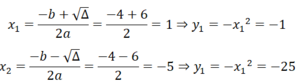Trên mặt phẳng tọa độ Oxy cho parabol (P): y=x2 và đường thẳng (d): y=2mx+1 (m là tham số)
1) Chứng minh rằng với mọi m thì đường thẳng (d) và parabol (P) cắt nhau tại 2 điểm phân biệt.
2) Gọi giao điểm của đường thẳng (d) và parabol (P) là A và B. Chứng minh tam giác OAB vuông.