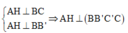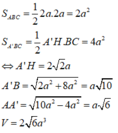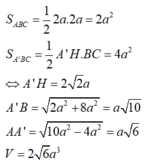cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A. Biết B'B=B'A=B'C=2a, AB=a. tínhchiều cao của lăng trụ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đây là toán lớp 12 à ./ sao dễ thế bây h tui mới biết kiến thức của mình lớp 12 cớ đấy ( nói zui thui)
câu 2
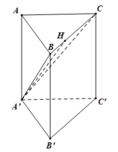
từ A hạ đường trung tuyến \(AM\perp BC\)( tam giác ABC zuông cân tại A)
từ B hạ\(BM\perp BC\)( tam giác B'BC cân tại B (gt)
=> M là hình chiếu của B' ( ABC)
=> B'M là đường cao
xét tam giác zuông MB'A zuông tại M
=>\(B'M^2+MA^2=AB'^2\Rightarrow B'M=\sqrt{AB'^2-MA^2}\)
ta lại có
\(\frac{1}{MA^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=>\frac{1}{MA^2}=\frac{1}{a^2}+\frac{1}{a^2}=>MA=\frac{a}{\sqrt{2}}\)
=> \(B'M=\sqrt{\left(2a\right)^2-\left(\frac{a}{\sqrt{2}}\right)^2}=\frac{a\sqrt{14}}{2}\)

Đáp án A
Diện tích tam giác ABC là S A B C = 1 2 A B 2 = a 2 2
Chiều cao của khối lăng trụ là V A B C . A ' B ' C ' = S A B C × h ⇒ h = 8 a 3
Ta có B C / / B ' C ' ⇒ d A B ; B ' C ' = d B ' C ' ; A B C = d B ' ; A B C = h = 8 a 3

Phương pháp:
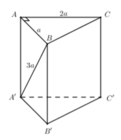
Sử dụng công thức tính thể tích lăng trụ V = S đ á y . h
Cách giải:
Trong tam giác vuông A'AB có:
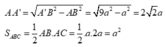
Vậy ![]()
Chọn: C